

Next: 6.3.3 Transient Simulation
Up: 6.3 Capacitance, Resistance and
Previous: 6.3.1 Capacitance Extraction
A current will flow between any pair of contacts at different electrical
potential (in a conductive material). Each electrically isolated conductor
can be treated as an individual problem whose solution involves solving
an equation similar to (6.1) to calculate the current
density and potential distribution. From those results, the resistance
is extracted using Ohm's law.
If 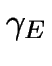 denotes the electrical
conductivity (assumed to be
denotes the electrical
conductivity (assumed to be 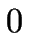 in all non-conductor materials), we obtain
in all non-conductor materials), we obtain
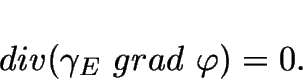 |
(6.2) |
For the thermal problem the resolution of
is required in all simulation domains. Here 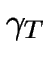 represents the
thermal conductivity,
represents the
thermal conductivity, 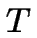 is the temperature distribution and
is the temperature distribution and
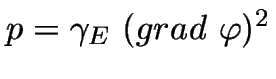 is the power loss density.
is the power loss density.
The electrical and thermal equations are linked by a first order
approximation given by
where 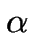 is a constant temperature
coefficient and
is a constant temperature
coefficient and 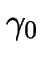 is
the electric conductivity at room temperature
is
the electric conductivity at room temperature 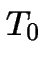 .
.


Next: 6.3.3 Transient Simulation
Up: 6.3 Capacitance, Resistance and
Previous: 6.3.1 Capacitance Extraction
Rui Martins
1999-02-24
![]() denotes the electrical
conductivity (assumed to be
denotes the electrical
conductivity (assumed to be ![]() in all non-conductor materials), we obtain
in all non-conductor materials), we obtain
![]() represents the
thermal conductivity,
represents the
thermal conductivity, ![]() is the temperature distribution and
is the temperature distribution and
![]() is the power loss density.
is the power loss density.
![]() is a constant temperature
coefficient and
is a constant temperature
coefficient and ![]() is
the electric conductivity at room temperature
is
the electric conductivity at room temperature ![]() .
.