Optical transition rules can be obtained from the optical matrix elements. The interband optical matrix element determines the probability for a transition from a state |m⟩ to a final state |n⟩ and is given by (q∕m0)⟨n|A⋅p|m⟩, [150] where q is the elementary charge, m0 is the electron mass, A = Aa is the vector potential, a is a unit vector parallel to A, and p is the linear momentum operator. The vector potential can be separated from the expectation value assuming the wave vector of the electromagnetic field is negligible compared to the electronic wave vector (dipole approximation). We have already used this approximation to derive the electron-photon interaction Hamiltonian (Eq. 3.10). As a result, optical matrix elements can be achieved by evaluating momentum matrix elements pn,m = ⟨n|px|m⟩. In this work the electromagnetic field is assumed to be polarized along the x direction.

Knowing the wave function of atomic orbitals, [173] the matrix elements of the momentum operator can be calculated from Eq. 3.13. However, in most of the tight-binding models the atomic orbitals are unknown, a difficulty which is usually circumvented by the gradient approximation [162], see Sec. 3.1.3. In this approximation intra-atomic transitions are ignored. However, as we employ a single orbital model to describe the electronic band-structure of ZGNRs, intra-atomic transitions are intrinsically neglected.
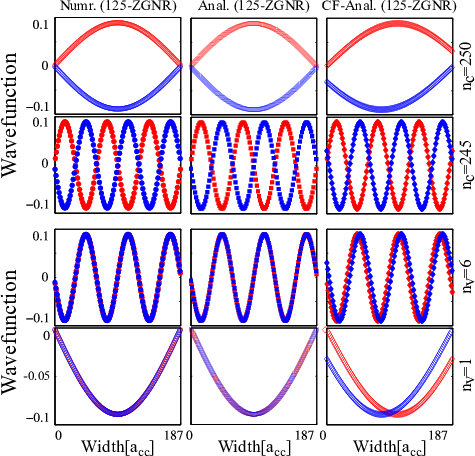
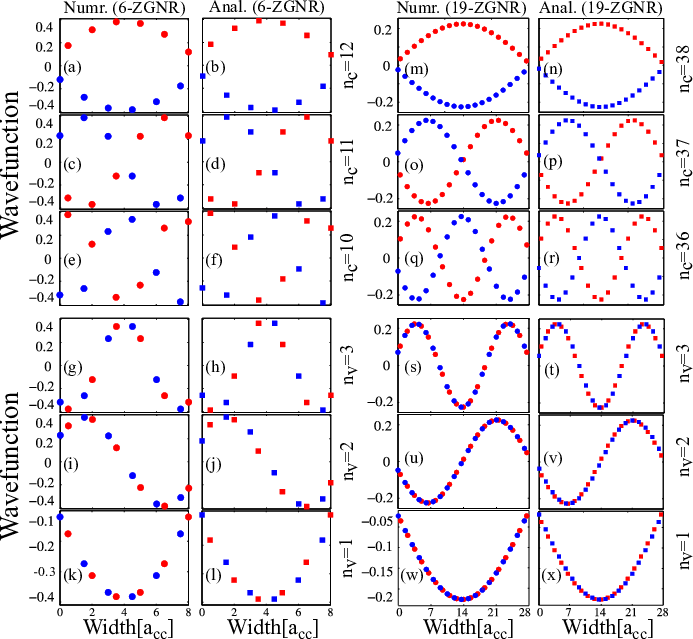
With the wave functions derived in the previous section, evaluation of transition rules from Eq. 3.13 is possible. Using the wave functions from Eq. 4.12 in Eq. 3.13, and considering only nearest neighbors, one can obtain (see Appendix B.3)
![( )
2√3m- a t √3-
Pθ,θ′ = ------0-cc-sin ---kacc
ℏ(2N + 1) 2
2N
∑ ′ ′
[sin(nθ )sin((2N - n + 1)θ) - sin(nθ) sin((2N - n + 1)θ )].
n=1](diss143x.png) | (4.29) |
The upper limit of summation 2N is due to degenerate points of valance and
conduction bands at kx = ±2π∕3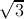 acc. The subband indices are included in θ and
θ′, see Eq. 4.28. The summation over sine functions in Eq. 4.29 determines the
transition rules. By some trigonometric identities one can rewrite this summation
as follows
acc. The subband indices are included in θ and
θ′, see Eq. 4.28. The summation over sine functions in Eq. 4.29 determines the
transition rules. By some trigonometric identities one can rewrite this summation
as follows
![√ -- ( √ -- )
--2--3m0acct- --3-
Pθ,θ′ = ℏ (2N + 1) sin 2 kacc
( ) ( )
cos (2N + 1)(θ + θ ′)∕2 sin 2N (θ - θ′)∕2
[-----------------------′-------------------
( sin((θ -′θ ))∕2) ( ′ )
cos (2N + 1)(θ - θ)∕2 sin 2N (θ + θ )∕2
- --------------sin-((θ-+-θ′)∕2)--------------].](diss145x.png) | (4.30) |
Using the analytical approximation of θ in Eq. 4.28 for the cosine terms in Eq. 4.30 gives
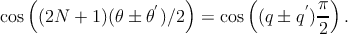 | (4.31) |
If q = 2r + 1 and q′ = 2r′ or q = 2r and q′ = 2r′ + 1 , where r and r′ are non-zero integers, q ± q′ = 2r′′ + 1, both terms in the bracket of Eq. 4.30 will be zero. In the case of q = 2r and q′ = 2r′ or q = 2r + 1 and q′ = 2r′ + 1, the terms in the bracket will be non zero. Therefore, the transitions between valence and conduction subbands only with the same parity (odd to odd and even to even) are allowed,
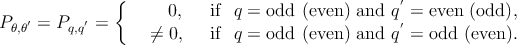 | (4.32) |