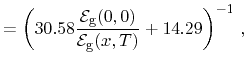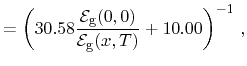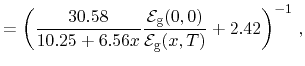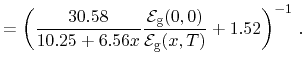5.3.2 Effective Masses, Density of States, Intrinsic Carrier Density
While the effective masses for each the first conduction and valence band of
lead telluride have been studied quite well in literature, only very uncertain
information is available for the second valence band. Both the valence and the
conduction band feature a strong anisotropy with material composition dependent
values of 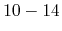 [260,188]. Values based on both measurements
as well as band structure calculations of the low temperature effective mass
for the first conduction and valence band, respectively are collected in
Table 5.8.
[260,188]. Values based on both measurements
as well as band structure calculations of the low temperature effective mass
for the first conduction and valence band, respectively are collected in
Table 5.8.
Table 5.8:
Low temperature effective masses for the first conduction and valence
band in lead telluride.
| Electrons |
Holes |
|
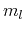
|
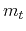
|
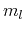
|
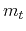
|
Ref. |
| 0.24 |
0.024 |
0.31 |
0.022 |
meas. [194] |
| 0.238 |
0.031 |
0.426 |
0.034 |
calc. [241] |
| 0.274 |
0.043 |
|
|
meas. [266] |
| |
|
0.165 |
0.030 |
meas. [267] |
| 0.24 |
0.022 |
|
|
meas. [199] |
| 0.23 |
0.022 |
|
|
calc. [199] |
|
The temperature dependence of the effective masses is commonly expressed by
quadratic polynomials [268]. According coefficients have been
identified based on temperature dependent data in [188]. Expressions
for the longitudinal and transversal effective masses for each the first
conduction and valence bands in pure lead telluride read
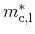 |
|
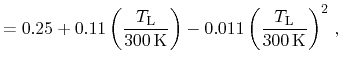 |
(5.26) |
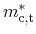 |
|
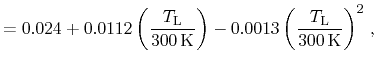 |
(5.27) |
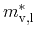 |
|
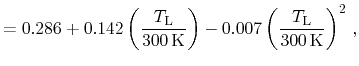 |
(5.28) |
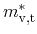 |
|
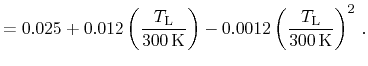 |
(5.29) |
The according temperature dependencies of the density-of-states masses derived
by
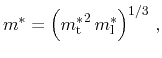 |
(5.30) |
have been identified as
Since the extrema of both the first conduction and valence band are located at
the L point, the number of equivalent valleys within the Brillouin zone
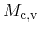 is 4. Thus, the effective density of states including spin-degeneracy can be
expressed by [269]
is 4. Thus, the effective density of states including spin-degeneracy can be
expressed by [269]
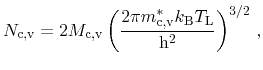 |
(5.33) |
and the intrinsic carrier concentration is derived as
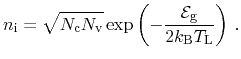 |
(5.34) |
Figure 5.10:
Temperature dependence of the effective density of states as well as
the intrinsic carrier concentration in lead telluride.
|
![\includegraphics[width=10cm]{figures/materials/PbTe/Ncv_ni.eps}](img752.png) |
Expressions for the material composition and temperature dependent effective
masses have been given by Preier [260] and Akimov
[202]. While both give expressions with respect to the temperature
and material composition dependent band gap, the latter does not differ between
the valence and conduction band and provides a constant anisotropy ratio
between the transversal and longitudinal effective masses. His expressions for
the relative carrier masses read
Preier differs between the according values of the valence and conduction
band and implies a material composition dependent anisotropy ratio
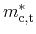 |
|
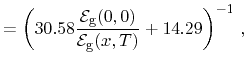 |
(5.37) |
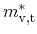 |
|
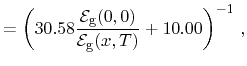 |
(5.38) |
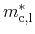 |
|
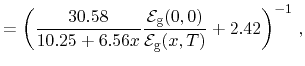 |
(5.39) |
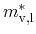 |
|
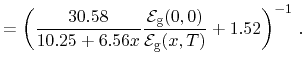 |
(5.40) |
M. Wagner: Simulation of Thermoelectric Devices
![]() [260,188]. Values based on both measurements
as well as band structure calculations of the low temperature effective mass
for the first conduction and valence band, respectively are collected in
Table 5.8.
[260,188]. Values based on both measurements
as well as band structure calculations of the low temperature effective mass
for the first conduction and valence band, respectively are collected in
Table 5.8.
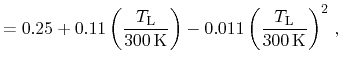
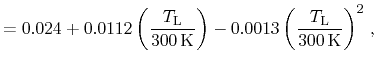
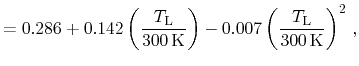
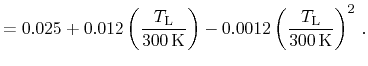
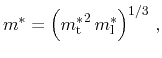
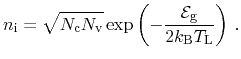
![\includegraphics[width=10cm]{figures/materials/PbTe/Ncv_ni.eps}](img752.png)