4.1.3 Introduction of Triangle Barycentric Coordinates

For the following explanation of edge elements exclusively barycentric coordinates will be used, because they offer advantages in understanding the following calculations. A point $P$ inside the triangle $123$ (Fig. <4.1>) divides this triangle into three sub triangles, namely $P12$ , $P23$ , and $P31$ , with the corresponding areas of these sub triangles $F_3$ , $F_1$ and $F_2$ . The barycentric coordinate $\lambda^e_i$ is the ratio of the area $F_i$ of the sub-face opposite to the i-th node to the whole area $F$ . Thus the barycentric coordinates are given by the following definitions (see Fig. <4.1>)

$$\begin{split}\lambda^e_1(\vec{r}) = \frac{F_1}{F_e} & = \frac... ...{r} - \vec{r}_B)\cdot\frac{l_{23}\cdot\vec{n}_1}{J} \end{split}$$ (4.30)

$$\lambda^e_2(\vec{r}) = \frac{F_2}{F_e} = \frac{1}{3} - (\vec{r} -... ..._z}{J} = \frac{1}{3} - (\vec{r} - \vec{r}_B)\cdot\frac{l_{31}\cdot\vec{n}_2}{J}$$ (4.31)

$$\lambda^e_3(\vec{r}) = \frac{F_3}{F_e} = \frac{1}{3} - (\vec{r} -... ...z}{J} = \frac{1}{3} - (\vec{r} - \vec{r}_B)\cdot\frac{l_{12}\cdot\vec{n}_3}{J},$$ (4.32)

where the following expressions have been used

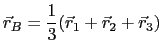$$\vec{r}_B = \frac{1}{3}(\vec{r}_1 + \vec{r}_2 + \vec{r}_3)$$ (4.33)

$$\vert\vec{r}_{12}\vert = l_{12}, \vert\vec{r}_{23}\vert = l_{23}, \vert\vec{r}_{31}\vert = l_{31}$$ (4.34)

$$\vec{r} = \vec{r}(x,y) = x \vec{e}_x + y \vec{e}_y.$$ (4.35)

$F_1$ , $F_2$ and $F_3$ are the areas of the triangles $P23$ , $P31$ and $P12$ , respectively

$$F_1 = F_{P23}, F_2 = F_{P31}, F_3 = F_{P12}.$$ (4.36)

This definition is very helpful for understanding of some of the following properties of the barycentric coordinates or linear element form functions, respectively.

The reason for the introduction of the barycentric coordinates at this place is, that they are identical to the linear triangular element shape functions. For instance, the expression for the barycentric coordinate $\lambda^e_1$ is given by

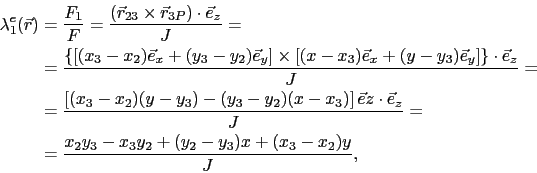$$\begin{split}\lambda^e_1(\vec{r}) & = \frac{F_1}{F} = \frac{(... ...{x_2y_3 - x_3y_2 + (y_2 - y_3)x + (x_3 - x_2)y}{J}, \end{split}$$ (4.37)

which complies with the first linear triangular element form function in (4.29). Thus the linear triangular barycentric coordinates and element shape functions use the same notation $\lambda_i^e$ .

The barycentric coordinate $\lambda^e_i$ is constant along a line parallel to the element edge opposite to the $i$ -th node and is zero on the opposite edge. Two barycentric coordinates are sufficient to determine the position of the point $P$ inside the triangle (see Fig. <4.1>). However, a third barycentric coordinate is introduced such that

$$\sum^3_{i=1}\lambda^e_i = 1.$$ (4.38)

Only two of the three linear element form functions are independent.

For the points inside the element and on the element edges it holds

$$0 \leq \lambda^e_1 \leq 1, 0 \leq \lambda^e_2 \leq 1, 0 \leq \lambda^e_3 \leq 1.$$ (4.39)

For points outside the element the barycentric coordinates can take arbitrary values. Of coarse (4.38) must be fulfilled. At least one and at most two barycentric coordinates must have negative values. This is illustrated in the example (Fig. <4.2>), where $\lambda_1^e$ and $\lambda_2^e$ are negative and $\lambda_3^e$ is greater than one. For instance, this relation can be used to determine, if a point lies inside or outside a given element. If there is at least one negative barycentric coordinate, the point lies outside. If one or two barycentric coordinates are zero, the point lies on the corresponding one or two edges of the element. Otherwise, if all are positive the point is inside.

Figure 4.2: Barycentric coordinates outside a triangular element.

Points located at a vertex of the element satisfy

$$\lambda^e_i(x_j,y_j) = \delta_{ij} = \left\{ \begin{array}{lc} 1 & i = j 0 & i \neq j \end{array} \right..$$ (4.40)

In the calculation of the finite elements also the gradients are needed. In barycentric coordinates the gradients are constant and expressed as

$$\begin{split}\vec{\nabla}\lambda^e_1(\vec{r}) & = - \frac{\ve... ...}_z}{J} = - \frac{l_{12}\cdot\vec{n}_3}{J} = const. \end{split}$$ (4.41)

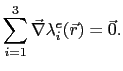$$\sum^3_{i=1}\vec{\nabla}\lambda^e_i(\vec{r}) = \vec{0}.$$ (4.42)

The coordinates of each point in the element are determined by

$$\vec{r} = \sum_{i=1}^3\lambda^e_i\vec{r}_i,$$ (4.43)

where $\lambda^e_1$ , $\lambda^e_2$ and $\lambda^e_3$ are the barycentric coordinates of the point inside the triangle element and $\vec{r}_1$ , $\vec{r}_2$ and $\vec{r}_3$ are the coordinates of the element vertices. Using (4.38) the expression (4.43) can be written as

$$\begin{split}x & = (x_1 - x_3)\lambda^e_1 + (x_2 - x_3)\lambd... ...1 - y_3)\lambda^e_1 + (y_2 - y_3)\lambda^e_2 + y_3. \end{split}$$ (4.44)

Equations (4.44) transform the local coordinates $\lambda_1^e$ and $\lambda_2^e$ to the global $xy$ coordinate system. Reversely each global element is mapped to the unit triangle in the $\lambda_1^e \lambda_1^e$ plane (Fig. <4.3>).

Figure 4.3: Two-dimensional domain transformation.

With the properties mentioned above the barycentric coordinates guarantee the continuity of the element interpolation function (4.29) across the element sides. For instance, on the Side $23$ the barycentric coordinates are restricted by

$$\lambda_1^e = 0 \mathrm{and} \lam... ...lambda_2^e \mathrm{(see Fig. {\tt <}\ref{fig:scalarfem2d_domtrans}{\tt >})}.$$

Thus the element interpolation function (4.29) on the Side $23$ is given by

$$\phi^e = \lambda_2^e \phi_2 + (1 - \lambda_2^e) \phi_3.$$ (4.45)

$\lambda_2^e(\vec{r})$ depends only on the position of $\vec{r}$ on the Edge $23$ . Thus for the two neighbor elements, which share the Edge $23$ , the corresponding element interpolation functions will be equal for the same position on Edge $23$ .