5.3.2 Assembling

$\begin{displaymath}\begin{split}S_{ij}^e & = \frac{1}{\gamma}\int_{\mathcal{A}_e... ...times\vec{N}_j^e\right)F_e, i\in[1;3], j\in[1;3], \end{split}\end{displaymath}$

(5.82)

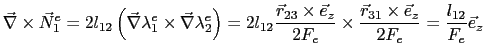$\displaystyle \vec{\nabla}\times\vec{N}_1^e = 2l_{12}\left(\vec{\nabla}\lambda_... ..._e}\times\frac{\vec{r}_{31}\times\vec{e}_z}{2F_e} = \frac{l_{12}}{F_e}\vec{e}_z$

(5.83)

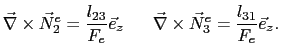$\displaystyle \vec{\nabla}\times\vec{N}_2^e = \frac{l_{23}}{F_e}\vec{e}_z \vec{\nabla}\times\vec{N}_3^e = \frac{l_{31}}{F_e}\vec{e}_z.$

(5.84)

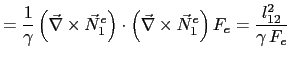$\displaystyle S_{11}^e$	$\displaystyle = \frac{1}{\gamma}\left(\vec{\nabla}\times\vec{N}_1^e\right) \cdot\left(\vec{\nabla}\times\vec{N}_1^e\right)F_e = \frac{l_{12}^2}{\gamma F_e}$	(5.85)
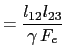$\displaystyle S_{21}^e = S_{12}^e$	$\displaystyle = \frac{l_{12}l_{23}}{\gamma F_e}$	(5.86)
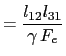$\displaystyle S_{31}^e = S_{13}^e$	$\displaystyle = \frac{l_{12}l_{31}}{\gamma F_e}$	(5.87)
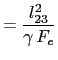$\displaystyle S_{22}^e$	$\displaystyle = \frac{l_{23}^2}{\gamma F_e}$	(5.88)
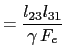$\displaystyle S_{32}^e = S_{23}^e$	$\displaystyle = \frac{l_{23}l_{31}}{\gamma F_e}$	(5.89)
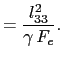$\displaystyle S_{33}^e$	$\displaystyle = \frac{l_{33}^2}{\gamma F_e}.$	(5.90)

$\displaystyle M_{ij}^e = \mu\int_{\mathcal{A}_e}\vec{N}_i^e\cdot\vec{N}_j^e \mathrm{d}A, i\in[1;3], j\in[1;3].$

(5.91)

$\begin{displaymath}\begin{split}M_{11}^e & = \mu\int_{\mathcal{A}_e}\vec{N}_1^e\... ..._e}\left(\lambda_2^e\right)^2 \mathrm{d}A \right]. \end{split}\end{displaymath}$

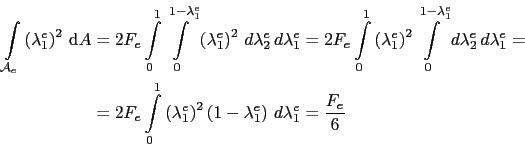$\begin{displaymath}\begin{split}\int_{\mathcal{A}_e}\left(\lambda_1^e\right)^2 ... ...(1-\lambda_1^e\right) d\lambda_1^e = \frac{F_e}{6} \end{split}\end{displaymath}$

(5.92)

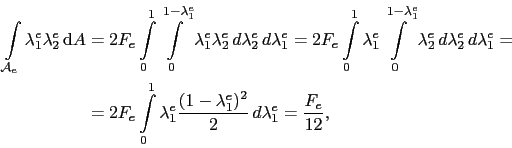$\begin{displaymath}\begin{split}\int_{\mathcal{A}_e}\lambda_1^e\lambda_2^e \mat... ...da_1^e\right)^2}{2} d\lambda_1^e = \frac{F_e}{12}, \end{split}\end{displaymath}$

(5.93)

$\displaystyle \int_{\mathcal{A}_e}\lambda_i^e\lambda_j^e \mathrm{d}A = \left\{... ...}{12} & \mathrm{for} i \neq j \end{array} \right. j\in[1;3], j\in[1;3].$

(5.94)

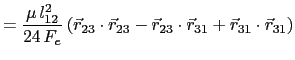$\displaystyle M_{11}^e$	$\displaystyle = \frac{\mu l_{12}^2}{24 F_e}\left(\vec{r}_{23}\cdot\vec{r}_{23} - \vec{r}_{23}\cdot\vec{r}_{31} + \vec{r}_{31}\cdot\vec{r}_{31}\right)$	(5.95)
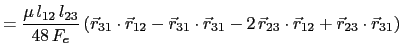$\displaystyle M_{21}^e = M_{12}^e$	$\displaystyle = \frac{\mu l_{12} l_{23}}{48 F_e}\left(\vec{r}_{31}\cdot\vec{... ..._{31} - 2 \vec{r}_{23}\cdot\vec{r}_{12} + \vec{r}_{23}\cdot\vec{r}_{31}\right)$	(5.96)
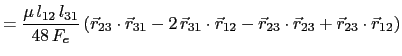$\displaystyle M_{31}^e = M_{13}^e$	$\displaystyle = \frac{\mu l_{12} l_{31}}{48 F_e}\left(\vec{r}_{23}\cdot\vec{... ...{r}_{12} - \vec{r}_{23}\cdot\vec{r}_{23} + \vec{r}_{23}\cdot\vec{r}_{12}\right)$	(5.97)
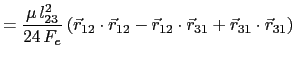$\displaystyle M_{22}^e$	$\displaystyle = \frac{\mu l_{23}^2}{24 F_e}\left(\vec{r}_{12}\cdot\vec{r}_{12} - \vec{r}_{12}\cdot\vec{r}_{31} + \vec{r}_{31}\cdot\vec{r}_{31}\right)$	(5.98)
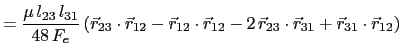$\displaystyle M_{32}^e = M_{23}^e$	$\displaystyle = \frac{\mu l_{23} l_{31}}{48 F_e}\left(\vec{r}_{23}\cdot\vec{... ..._{12} - 2 \vec{r}_{23}\cdot\vec{r}_{31} + \vec{r}_{31}\cdot\vec{r}_{12}\right)$	(5.99)
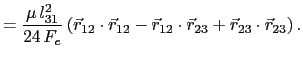$\displaystyle M_{33}^e$	$\displaystyle = \frac{\mu l_{31}^2}{24 F_e}\left(\vec{r}_{12}\cdot\vec{r}_{12} - \vec{r}_{12}\cdot\vec{r}_{23} + \vec{r}_{23}\cdot\vec{r}_{23}\right).$	(5.100)

$\displaystyle B_{ij}^e = - \jmath\omega\mu\int_{\mathcal{A}_e}\vec{N}_i^e\cdot\vec{\nabla}\lambda_j^e \mathrm{d}A, i\in[1;3], j\in[1;3].$

(5.101)

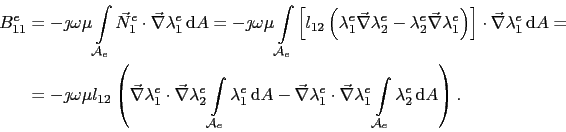$\begin{displaymath}\begin{split}B_{11}^e & = - \jmath\omega\mu\int_{\mathcal{A}_... ...nt_{\mathcal{A}_e}\lambda_2^e \mathrm{d}A \right). \end{split}\end{displaymath}$

(5.102)

$\displaystyle \int_{\mathcal{A}_e}\lambda_i^e \mathrm{d}A = \frac{F_e}{3}, i\in[1;3].$

(5.103)

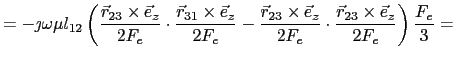$\displaystyle B_{11}^e$	$\displaystyle = - \jmath\omega\mu{}l_{12} \left(\frac{\vec{r}_{23}\times\vec{e}... ...e}_z}{2F_e}\cdot\frac{\vec{r}_{23}\times\vec{e}_z}{2F_e} \right)\frac{F_e}{3} =$	(5.104)
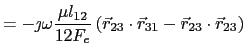	$\displaystyle = - \jmath\omega\frac{\mu{}l_{12}}{12F_e} \left( \vec{r}_{23}\cdot\vec{r}_{31} - \vec{r}_{23}\cdot\vec{r}_{23} \right)$
$\displaystyle B_{12}^e$	$\displaystyle = - \jmath\omega\frac{\mu{}l_{12}}{12F_e} \left( \vec{r}_{31}\cdot\vec{r}_{31} - \vec{r}_{31}\cdot\vec{r}_{23} \right)$	(5.105)
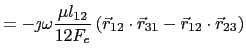$\displaystyle B_{13}^e$	$\displaystyle = - \jmath\omega\frac{\mu{}l_{12}}{12F_e} \left( \vec{r}_{12}\cdot\vec{r}_{31} - \vec{r}_{12}\cdot\vec{r}_{23} \right)$	(5.106)
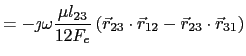$\displaystyle B_{21}^e$	$\displaystyle = - \jmath\omega\frac{\mu{}l_{23}}{12F_e} \left( \vec{r}_{23}\cdot\vec{r}_{12} - \vec{r}_{23}\cdot\vec{r}_{31} \right)$	(5.107)
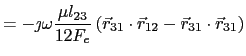$\displaystyle B_{22}^e$	$\displaystyle = - \jmath\omega\frac{\mu{}l_{23}}{12F_e} \left( \vec{r}_{31}\cdot\vec{r}_{12} - \vec{r}_{31}\cdot\vec{r}_{31} \right)$	(5.108)
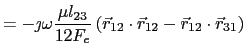$\displaystyle B_{23}^e$	$\displaystyle = - \jmath\omega\frac{\mu{}l_{23}}{12F_e} \left( \vec{r}_{12}\cdot\vec{r}_{12} - \vec{r}_{12}\cdot\vec{r}_{31} \right)$	(5.109)
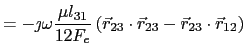$\displaystyle B_{31}^e$	$\displaystyle = - \jmath\omega\frac{\mu{}l_{31}}{12F_e} \left( \vec{r}_{23}\cdot\vec{r}_{23} - \vec{r}_{23}\cdot\vec{r}_{12} \right)$	(5.110)
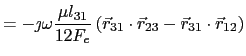$\displaystyle B_{32}^e$	$\displaystyle = - \jmath\omega\frac{\mu{}l_{31}}{12F_e} \left( \vec{r}_{31}\cdot\vec{r}_{23} - \vec{r}_{31}\cdot\vec{r}_{12} \right)$	(5.111)
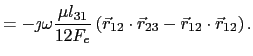$\displaystyle B_{33}^e$	$\displaystyle = - \jmath\omega\frac{\mu{}l_{31}}{12F_e} \left( \vec{r}_{12}\cdot\vec{r}_{23} - \vec{r}_{12}\cdot\vec{r}_{12} \right).$	(5.112)

$\displaystyle C_{11}^e$	$\displaystyle = -\jmath\omega\frac{\mu}{4F_e} \vec{r}_{23}\cdot\vec{r}_{23}$	(5.113)
$\displaystyle C_{12}^e = C_{21}^e$	$\displaystyle = -\jmath\mu\frac{\mu}{4F_e} \vec{r}_{23}\cdot\vec{r}_{31}$	(5.114)
$\displaystyle C_{13}^e = C_{31}^e$	$\displaystyle = -\jmath\mu\frac{\mu}{4F_e} \vec{r}_{23}\cdot\vec{r}_{12}$	(5.115)
$\displaystyle C_{22}^e$	$\displaystyle = -\jmath\omega\frac{\mu}{4F_e} \vec{r}_{31}\cdot\vec{r}_{31}$	(5.116)
$\displaystyle C_{23}^e = C_{32}^e$	$\displaystyle = -\jmath\omega\frac{\epsilon}{4F_e} \vec{r}_{31}\cdot\vec{r}_{12}$	(5.117)
$\displaystyle C_{33}^e$	$\displaystyle = -\jmath\omega\frac{\mu}{4F_e} \vec{r}_{12}\cdot\vec{r}_{12}.$	(5.118)