![\includegraphics[width=14cm]{figures/appendix/intdomtrans.eps}](img752.gif) |
It has been shown that the barycentric coordinates transform each triangular and tetrahedron element in the unit triangle and tetrahedron, respectively. (Refer to Fig. <4.3> and Fig. <4.8>.) This is used for the analytical calculation of the arising integral terms, when the element matrices are assembled.
The two-dimensional domain
![]() is transformed to
is transformed to
![]() by
the expressions
by
the expressions
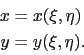 |
(A.1) |
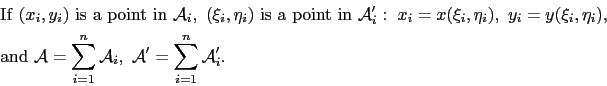 |
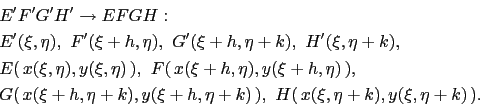 |
(A.2) |
The area ![]() of the
of the ![]() -th element
-th element ![]() is approximately related by
the vector product
is approximately related by
the vector product
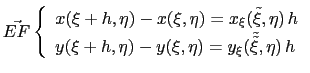 |
(A.3) |
and
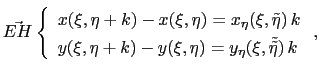 |
(A.4) |
where
| (A.5) |
For sufficiently small ![]() and
and ![]() the face
the face ![]() is expressed as
is expressed as
![\begin{displaymath}\begin{split}A_i & = \vert\vec{EF}\times\vec{EH}\vert = [x_{\...
...xi,\eta)]\vert hk\vert = J(\xi, \eta) A_i^{\prime} \end{split}\end{displaymath}](img761.gif) |
(A.6) |
with
Analogously the transformation for the three-dimensional case can be expressed by:
with