3.1.4 Carrier Lifetime

The carrier lifetime (recombination lifetime) is defined as the average time it takes an excess minority carrier to recombine. As mentioned in the previous section, three recombination mechanisms - band-to-band, trap-assisted (or SRH) and Auger recombinations - determine the recombination lifetime. Band-to-band recombination is relatively unimportant in silicon, because its radiative lifetime is extremely high. Auger lifetime is independent of any impurity density. However, it is inversely proportional to the carrier density. SRH recombination is determined by the amount of impuities and defects in the silicon. Therefore, at high carrier densities, the recombination lifetime in silicon is controlled by Auger recombination and at low carrier densities by SRH recombination. The minority carrier lifetime in heavily doped

- and

-type material is related to the capture rate for electrons and holes at the recombination center. In addition it is a function of the doping concentration, because additional traps are created at high doping level.

For the SRH recombination the minority carrier lifetimes $\tau_n$ and $\tau_p$ can be shown as:

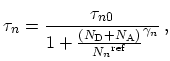$\displaystyle \tau_n = \frac{\tau_{n0}}{1 + \frac{(N_\mathrm{D} + N_\mathrm{A})}{{N_n}^{\mathrm{ref}}}^{\gamma_n }}\,,$

(3.17)

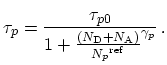$\displaystyle \tau_p = \frac{\tau_{p0}}{1 + \frac{(N_\mathrm{D} + N_\mathrm{A})}{{N_p}^{\mathrm{ref}}}^{\gamma_p }}\,.$

(3.18)

where $N_n^{\mathrm{ref}}$ , $N_p^{\mathrm{ref}}$ , $\gamma_n$ , and $\gamma_p$ are fitting parameters for electrons and holes, respectively [18]. $\tau_{n0}$ and $\tau_{p0}$ are the electron and hole minority carrier life times at low doping levels, respectively. The carrier lifetime is very sensitive to the fabrication procedure, and it is very difficult to determine this value without any measurement data. One way to determine the lifetime is to measure the capture cross-sections and the positions of the recombination (deep level) center in the band gap. At low injection levels the lifetime $\gamma_{\scriptstyle{LL}}$ depends on the deep level position in the band gap and the capture cross-section ratio $\zeta$

$\tau_{n0}$

$\tau_{p0}$ .

**Figure 3.3:** Change in minority carrier lifetime with injection level.
$\begin{figure}\begin{center} \psfig{file=figures/addition/impact/normal_lifetime.eps, width=0.7\linewidth} \vspace{0.0cm} \end{center}\end{figure}$

Figure 3.3 shows the variation in the lifetime with normalized injection level $\delta n$

(where $\delta n$ is an excess electron concentration and

is an equilibrium concentration of electron) for the

-type silicon for doping concentration of 1 $\times$ $10^{14}$ $\mathrm{cm^{-3}}$ . In Figure 3.3, capture cross-section ratio $\zeta$ and deep level in the energy gap $E_\mathrm{r}$ are considered. At low injection level ( $\delta n$

1) the lifetime is dependent upon the deep level position $E_\mathrm{r}$ and capture cross-section ratio $\zeta$ . It has a minimum when the recombination center lies close to middle of the band gap ( $E_\mathrm{r}$

0.555 in Figure 3.3). On the other hand, the high level lifetime $\gamma_{\scriptstyle{HL}}$ approaches a constant value. It is not dependent upon the position of the deep level, but it depends on the capture cross-section ratio $\zeta$ [59]

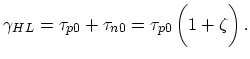$\displaystyle \gamma_{\scriptstyle{HL}} = \tau_{p0} + \tau_{n0} = \tau_{p0}\, \biggl( 1 + \zeta \biggr)\,.$

(3.19)

The recombination rates of majority carriers equals that of minority carriers, because a recombination process involves an equal number of holes and electrons.

The generation lifetime $\tau_{sc}$ in a space charge region where the hole and electron concentration are close to each other can be derived from the SRH recombination generation equation

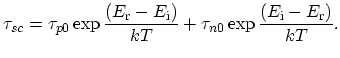$\displaystyle \tau_{sc} = \tau_{p0}\, \mathrm{exp}\,\frac{(E_\mathrm{r} - E_\ma... ...} )}{kT} + \tau_{n0}\, \mathrm{exp}\,\frac{(E_\mathrm{i} - E_\mathrm{r} )}{kT}.$

(3.20)

For bipolar power devices a small low level lifetime is highly desirable to obtain fast switching performance. On the other hand, a large high level lifetime is desirable to obtain high current density during on-state. In addition a lower space charge generation lifetime produces a higher leakage current. For obtaining the best trade-off among the device characteristics, such as switching speed, on-state current, and leakage current, it is important to find an optimal location of a deep level position and its capture cross-section. Several methods can be applied to control the carrier lifetime of bipolar power devices (gold and platinum diffusions, electron or proton irradiations, gamma-ray irradiation, etc.).

The variation in the lifetime with temperature is also important for power devices operating at a high temperature. From measurements of the recombination lifetime in power devices it was concluded that the lifetime increases with rising temperature. We assume a simple power law for the temperature dependence of the carrier lifetime

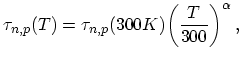$\displaystyle \tau_{n,p} (T) = \tau_{n,p} (300K) \biggl(\frac{T}{300} \biggr)^{\alpha}\,,$

(3.21)