3.2.1.1 Avalanche Generation

In order to compute the BV, it is necessary to determine the condition under which the impact ionization achieves an infinite rate. Generation of electron-hole pairs due to impact ionization requires a certain threshold energy (approximately 3.6eV for electrons and 5.0eV for holes in silicon) and the possibility of acceleration of the energy of electrons and holes, i.e. wide space charge regions. If the width of the space charge region is larger than the mean free path of carriers, charge multiplication occurs, which can cause electrical breakdown.

**Figure 3.5:** Reverse biased junction.
$\begin{figure}\begin{center} \psfig{file=figures/chapt3/parallel-pn.eps, width=0.7\linewidth} \vspace{0.0cm} \end{center}\end{figure}$

Consider a reverse-biased parallel-plane -junction with a positive bias applied to the -region (see Figure 3.5) . Under the influence of the electric field in the depletion region, the electron will be swept towards the -region and the hole will be swept towards the region. Using the definitions for the ionization coefficients, the hole will create $\alpha_p\,dx$ electron-hole pairs after traveling a distance and the electron will create $\alpha_n\,dx$ electron-hole pairs. The total number of electron-hole pairs created in the depletion region by a single electron-hole pair generated at a distance is given by

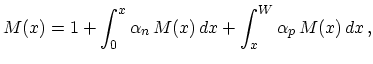$\displaystyle M(x) = 1 + \int_0^x \alpha_n\, M(x)\,dx + \int_x^W \alpha_p\, M(x)\,dx\,,$

(3.26)

where is the depletion layer width. The integrations are performed along field lines through the depletion region. A solution of this integral equation is

$\displaystyle M(x) = \frac{\mathrm{exp}\,[\int_0^x (\alpha_n - \alpha_p)\,dx]} {1 - \int_x^W \alpha_p\, \mathrm{exp}\,[\int_0^x (\alpha_n - \alpha_p)\,dx]\,dx}.$

(3.27)

is commonly known as the multiplication coefficient. The breakdown voltage is defined as the voltage at which reaches infinity. It occurs if the following integral equals one

$\displaystyle \int_x^W \alpha_p\, \mathrm{exp}\,[\int_0^x (\alpha_n - \alpha_p)\,dx]\,dx = 1,$

(3.28)

where the left-hand side of (3.28) is known as the ionization integral. With the approximation given in (3.25) the avalanche breakdown condition corresponds to

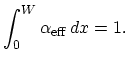$\displaystyle \int_0^W \alpha_\mathrm{eff}\,dx = 1.$

(3.29)

Jong-Mun Park 2004-10-28