


Next: 4.1.4 Newton Direction
Up: 4.1 Optimization Methods
Previous: 4.1.2 Step direction
4.1.3 Steepest-descent
The modeling of the target function can be done by a
linear approximation of 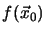 based on a Taylor-series
expansion of first order
based on a Taylor-series
expansion of first order
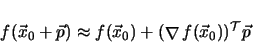 |
(4.6) |
where 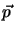 denotes a small step away from the current point
denotes a small step away from the current point 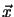 .
A reduction of the function can be achieved by a step
.
A reduction of the function can be achieved by a step 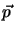 where
where
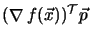 is a
negative number with a large absolute value. The direction can be
found by solving the following minimization problem
is a
negative number with a large absolute value. The direction can be
found by solving the following minimization problem
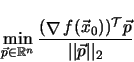 |
(4.7) |
which gives direction 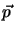
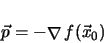 |
(4.8) |
along the negative gradient of the target function f.
R. Plasun
![]() based on a Taylor-series
expansion of first order
based on a Taylor-series
expansion of first order
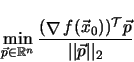
![]()