4.8.2 Non-adaptive Energy Grid
One can straightforwardly divide the integration domain into
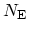 equidistant intervals
equidistant intervals
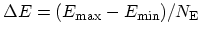 . A disadvantage of this method
is that the numerical error can not be pre-defined. This problem is more
pronounced when the integrand is not smooth. To evaluate (4.60)
numerically a trapezoidal rule and an equidistant grid spacing are used. The
dependence of the accuracy on the following two parameters is studied, namely the grid
spacing,
. A disadvantage of this method
is that the numerical error can not be pre-defined. This problem is more
pronounced when the integrand is not smooth. To evaluate (4.60)
numerically a trapezoidal rule and an equidistant grid spacing are used. The
dependence of the accuracy on the following two parameters is studied, namely the grid
spacing, 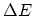 , and the relative distance between the peak and the nearest
grid point,
, and the relative distance between the peak and the nearest
grid point, 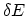 . These parameters are normalized as
. These parameters are normalized as
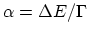 and
and
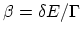 . The
relative error in calculating the carrier concentration,
. The
relative error in calculating the carrier concentration,
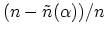 , as a function of grid spacing is shown
in Fig. 4.10. Here,
, as a function of grid spacing is shown
in Fig. 4.10. Here, 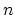 is the analytically exact value of the carrier
concentration (4.60) and
is the analytically exact value of the carrier
concentration (4.60) and 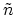 refers to the numerically
calculated carrier concentration as a function of
refers to the numerically
calculated carrier concentration as a function of 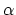 and
and 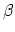 .
.
The variation of the calculated carrier concentration
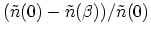 with respect to the shift
of energy points is shown in Fig. 4.11. The reference
with respect to the shift
of energy points is shown in Fig. 4.11. The reference 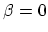 implies
that one of the grid points aligns with the peak of the resonance. The
oscillatory behavior depends on the grid spacing. A shift equal to the
grid spacing gives the same result.
As a measure of the sensitivity of the calculated carrier concentration with respect to
grid positions
implies
that one of the grid points aligns with the peak of the resonance. The
oscillatory behavior depends on the grid spacing. A shift equal to the
grid spacing gives the same result.
As a measure of the sensitivity of the calculated carrier concentration with respect to
grid positions
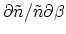 is shown in Fig. 4.12. To
reduce this sensitivity, a very fine grid spacing has to be adopted. This
quantity is characteristic of the numerical error, and needs to be controlled to avoid
convergence problem in the self-consistent iteration loop (see Section 4.9.2).
is shown in Fig. 4.12. To
reduce this sensitivity, a very fine grid spacing has to be adopted. This
quantity is characteristic of the numerical error, and needs to be controlled to avoid
convergence problem in the self-consistent iteration loop (see Section 4.9.2).
Figure 4.10:
The relative error in evaluating the carrier concentration
with respect to the grid spacing is shown.
The inset shows the normalized LORENTZian shape of the density of states
of a bound state. The peak of the resonance is shifted
to the zero point. At E=
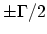 the function is half of its
maximum. The solid line shows the exact function and the dashed curve shows
the approximation of the function based on the Trapezoidal rule. The grid
spacing is
the function is half of its
maximum. The solid line shows the exact function and the dashed curve shows
the approximation of the function based on the Trapezoidal rule. The grid
spacing is 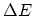 and the shift of energy grids from the reference
point is
and the shift of energy grids from the reference
point is 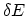 . These parameters are normalized as
. These parameters are normalized as
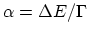 and
and
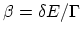 . The reference
. The reference 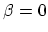 implies
that the one of the grid points aligns with the peak of the resonance. The
parameters in this figure are
implies
that the one of the grid points aligns with the peak of the resonance. The
parameters in this figure are
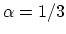 and
and 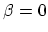 .
.
|
|
Figure 4.11:
The relative variation of the
calculated carrier concentration with respect to the
normalized position 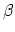 of energy grid points.
of energy grid points.
|
|
Figure 4.12:
The relative sensitivity of the
calculated carrier concentration
with respect to the position of energy grid points. This term originates
from the numerical error in the evaluation of the
carrier concentration. For coarse grid spacing 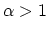 , this quantity
increases considerably.
, this quantity
increases considerably.
|
|
In summary, the accuracy of the non-adaptive method strongly depends on the grid
spacing and the position of grid points. If the grid spacing is sufficiently
fine, 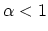 , the numerical error is small, but it increases considerably
for coarser grid spacing,
, the numerical error is small, but it increases considerably
for coarser grid spacing, 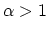 . For accurate results a grid spacing
smaller than
. For accurate results a grid spacing
smaller than 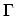 has to be employed. For example, to resolve a resonance
of
has to be employed. For example, to resolve a resonance
of
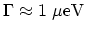 width in an energy range of
width in an energy range of
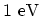 more than
more than
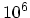 energy grid points are required,
which would severely increase the computational cost. For even narrower
resonances, (eg.
energy grid points are required,
which would severely increase the computational cost. For even narrower
resonances, (eg.
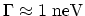 ), an equidistant grid is no
longer feasible. To avoid these problems an adaptive method needs to be
employed.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
), an equidistant grid is no
longer feasible. To avoid these problems an adaptive method needs to be
employed.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() with respect to the shift
of energy points is shown in Fig. 4.11. The reference
with respect to the shift
of energy points is shown in Fig. 4.11. The reference ![]() implies
that one of the grid points aligns with the peak of the resonance. The
oscillatory behavior depends on the grid spacing. A shift equal to the
grid spacing gives the same result.
As a measure of the sensitivity of the calculated carrier concentration with respect to
grid positions
implies
that one of the grid points aligns with the peak of the resonance. The
oscillatory behavior depends on the grid spacing. A shift equal to the
grid spacing gives the same result.
As a measure of the sensitivity of the calculated carrier concentration with respect to
grid positions
![]() is shown in Fig. 4.12. To
reduce this sensitivity, a very fine grid spacing has to be adopted. This
quantity is characteristic of the numerical error, and needs to be controlled to avoid
convergence problem in the self-consistent iteration loop (see Section 4.9.2).
is shown in Fig. 4.12. To
reduce this sensitivity, a very fine grid spacing has to be adopted. This
quantity is characteristic of the numerical error, and needs to be controlled to avoid
convergence problem in the self-consistent iteration loop (see Section 4.9.2).
![\includegraphics[width=0.45\textwidth]{figures/na.eps}](img897.png)
![\includegraphics[width=0.43\textwidth]{figures/nb.eps}](img898.png)
![\includegraphics[width=0.43\textwidth]{figures/dnb.eps}](img899.png)