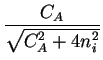

Next: 2.1.2 Pair-Diffusion Mechanism
Up: 2.1 Diffusion
Previous: 2.1 Diffusion
At usual diffusion temperatures the dopants are often ionized and the
so released electrons cause an electric field which operates as an
additional drift term to the normal diffusion flux.
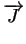 = - D . grad (C) +
= - D . grad (C) + 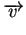 . C . C |
|
|
(2.4) |
The velocity of the charged particles can be described
with
where
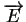 is the electric field and
is the electric field and
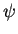 the electrostatic potential. The mobility
the electrostatic potential. The mobility 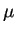 is related to the
diffusion coefficient by Einstein's relation
is related to the
diffusion coefficient by Einstein's relation
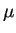 = D .
= D . 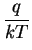 |
|
|
(2.6) |
where q denotes the elementary charge and k is known as the
Boltzmann constant.
Introducing (2.6) and (2.5) into
(2.4) and taking more than one dopant into account Fick's
law can be extended to
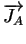 = - DA .
= - DA .  grad (CA) + zA . grad (CA) + zA . 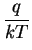 . CA . grad ( . CA . grad (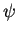 ) )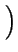 |
|
|
(2.7) |
where zA denotes the charge state of the belonging dopant (+1
for singly charged acceptors and -1 for singly charged donors).
The electrostatic potential 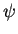 is determined by the Poisson equation
is determined by the Poisson equation
div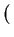 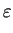 . grad ( . grad (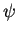 ) ) = q . (n - p - Cnet)
= q . (n - p - Cnet) |
|
|
(2.8) |
with
Cnet = - 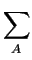 zA . CA zA . CA |
|
|
(2.9) |
where the quantity Cnet represents the net concentration of all ionized
dopants and n, p the concentration of electrons and holes, respectively.
Under the assumption of thermodynamic equilibrium the carrier
concentrations n and p can be obtained with
| n . p = ni2 |
|
|
(2.10) |
n = ni . e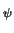 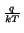 |
|
|
(2.11) |
p = ni . e- 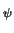 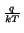 |
|
|
(2.12) |
In case of global charge neutrality
and by means of the equilibrium carrier concentrations
(2.11)(2.12) the electrostatic potential can explicitly
be calculated by
With the explicit form of the gradient of 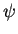 ,
,
grad (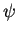 ) = - ) = - 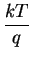 . . 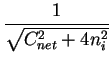 . . 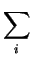 zi . Ci zi . Ci |
|
|
(2.15) |
substituting into (2.7) the flux
for dopant CA now depends also on the gradients of the concentrations Ci
of all other dopants.
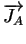 = - DA .
= - DA .  1 + 1 + 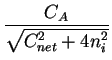
 . grad (CA) - . grad (CA) - |
|
|
|
DA . 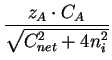 . . 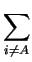 zi . grad (Ci) zi . grad (Ci) |
|
|
(2.16) |
If only one dopant is present (2.16) simplifies to
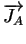 = - DA .
= - DA . 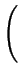 1 + 1 + 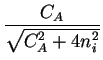
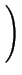 . grad (CA) . grad (CA) |
|
|
(2.17) |
Comparing Fick's first law (2.1) and
(2.17) an effective diffusion coefficient with the field enhancement factor 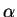 can be extracted
can be extracted
Deff = DA . 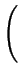 1 + 1 + 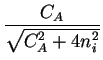
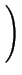 =
= 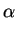 . DA . DA |
|
|
(2.18) |
For intrinsic conditions (
CA/ni 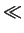 1) this factor has a value
close to one and for high concentrations (
CA/ni
1) this factor has a value
close to one and for high concentrations (
CA/ni 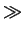 1) a value close to two.
1) a value close to two.


Next: 2.1.2 Pair-Diffusion Mechanism
Up: 2.1 Diffusion
Previous: 2.1 Diffusion
Mustafa Radi
1998-12-11
![]() is determined by the Poisson equation
is determined by the Poisson equation
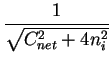 .
. ![]() can be extracted
can be extracted