

Next: 2.2.2 Point Defect Models
Up: 2.2 Oxidation
Previous: 2.2 Oxidation
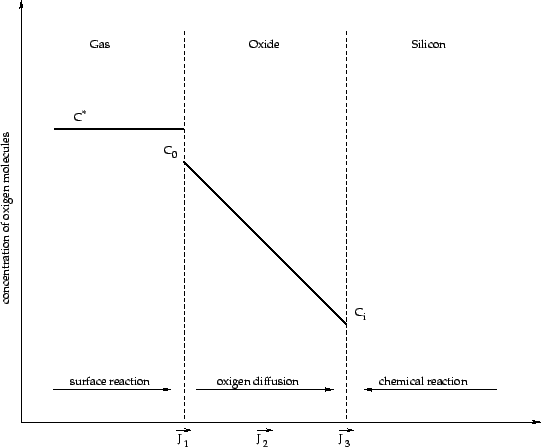
In 1965 Deal & Grove [Dea65] published the first reasonable attempt to
describe thermal oxidation including three mechanisms to handle the
known effects (Fig. 2.3):
- surface reaction of surrounding atmosphere
- diffusion process through existing oxide towards the interface between silicon and silicon dioxide
- chemical reaction of silicon and oxygen atoms
Figure 2.3:
Model for oxide growth suggested by Deal & Grove
|
|
At first, each of these steps can be described as independent flux
equation, where the surface reaction can be written as
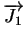 = h1 . (C
= h1 . (C - C0) - C0) |
|
|
(2.25) |
where C represents the concentration of oxygen in the surrounding gas,
C0 the concentration at the oxide interface and h1 a surface transport
coefficient.
represents the concentration of oxygen in the surrounding gas,
C0 the concentration at the oxide interface and h1 a surface transport
coefficient.
The diffusion is handled after Fick's law described in
Chapter 2.1
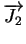 = - D . grad (C)
= - D . grad (C) |
|
|
(2.26) |
and finally the chemical reaction at the silicon/ silicon dioxide interface
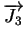 = h2 . Ci
= h2 . Ci |
|
|
(2.27) |
with h2 as reaction ratio of the oxidation process. Thus, the oxide
growth rate is equal to the rate of oxidizing molecules F reacting
at the interface, divided by the number of oxide molecules N being
incorporated to form a unit volume of oxide. Assuming equilibrium
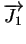 =
= 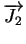 =
= 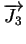 =
=  the one-dimensional oxidation ratio can be written as
the one-dimensional oxidation ratio can be written as
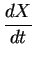 =
= 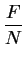 |
|
|
(2.28) |
where X denotes the oxide thickness. After eliminating Ci and C0
using (2.25), (2.26)
and (2.27), a differential equation of the form
can be found with the parameters
A = 2D . 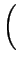 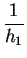 +
+ 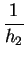
 |
|
|
(2.30) |
B = 2D . 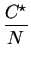 . . |
|
|
(2.31) |
The analytic solution of this differential equation with the start
condition X = 0 at t = 0 is a quadratic equation of the form
X2 + A . X = B . t or 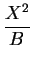 +
+ 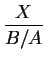 = t.
= t. |
|
|
(2.32) |
with the explicit result for the oxide thickness depending on time
Looking at the solution two different limiting values are recognizable.
On the one hand, for long oxidation times (
t  A2/4B) an approximately
parabolic growth law
A2/4B) an approximately
parabolic growth law
X = 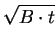 |
|
|
(2.34) |
can be established and, on the other hand, for
very short oxidation times (
t  A2/4B) a nearly linear trend of
the oxidation growth with
A2/4B) a nearly linear trend of
the oxidation growth with
X = 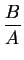 . t . t |
|
|
(2.35) |
can be assumed.
Although the model of Deal & Grove was found in 1965 it was not
possible to explain the parameters A and B on physical basics and,
therefore, they are just known as fitting parameters. Furthermore, for
very small oxide thickness sizes (X < 35 nm) the model does not fit
the experimental data. Unfortunately, these sizes are of increasing
importance since device sizes of transistors are dramatically
shrinking. Nevertheless, in practice this model is more or less
exclusively used to simulate the oxidation phenomena, where the
parameters (Table 2.3)
are often calculated after Arrhenius' law:
B = B0 . e- 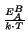 |
|
|
(2.36) |
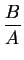 =
=  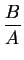
 . e- . e- 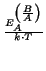 |
|
|
(2.37) |
Since the parameter values are varying in a wide range, and no
physical description was found, a lot of tries to find an adequate
model for oxidation have been made during the last 30 years, but till
now with limited success.


Next: 2.2.2 Point Defect Models
Up: 2.2 Oxidation
Previous: 2.2 Oxidation
Mustafa Radi
1998-12-11

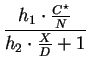 =
= 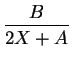
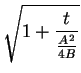 - 1
- 1