4.3.2.1 Analytical Model Optimizer

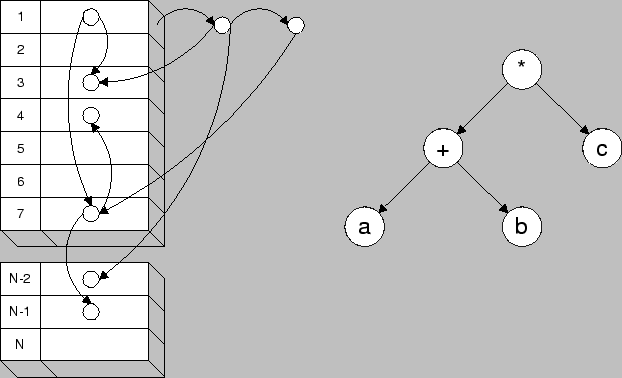
The Analytical Model Interface is designed in a way that every mathematical expression is represented with a tree structure that is assembled into an extendible hash shown in Fig. 4.6. The hash table is used for fast search purposes to reuse once calculated subtrees. Furthermore, trivial operations such as multiplying by one or zero, or adding or subtracting zero are eliminated to minimize the number of calculations during model evaluation.

Figure 4.6: Extendible hash representing mathematical expressions such as the tree representing (a+b)*c

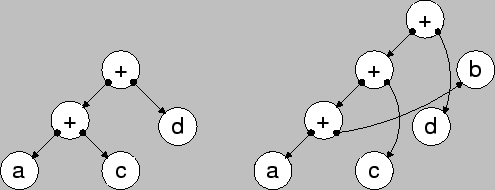
A further advantage of using this internal representation is the possibility to solve the general problem of permutations of some operators (e.g. distributive law) in a very fast manner without searching for equality of permutative terms. The simple but effective mechanism of key calculation of a hash table offers the possibility to get rid of the severe problem of permutations. Consider a simple example where N variables are to be added a₁ + a₂ + ... + a_N. This results in N! possible trees to represent this problem. To search an already existing tree would need an unacceptable amount of time and therefore a different mechanism must be found to optimize the tree. The best approach to get rid of this problem is simply avoiding the search mechanism by using a specific way of tree assembling, which guarantees a definite combination of the resulting tree. In other words, no matter in which order the N variables are given the resulting tree must always be the same. This condition can be satisfied by calculating a hash key of a node and depending on the result a simple recursive reorganization of the tree has to be done (Fig. 4.7).

Figure 4.7: Insertion of a variable b into an existing tree (a+c+d) which needs reorganization to avoid permutation problems (resulting order: a+b+c+d)