|
To solve complex PDE systems a lot of different strategies are necessary to minimize the amount of memory and calculation time. The optimization of the analytical PDE models, which has already been discussed in the previous sections, is only one opportunity out of a set of possibilities. To increase the performance and convergence of a simulation step it is also necessary to consider the resulting global stiffness matrices that are assembled automatically by AMIGOS.
Since AMIGOS can manage several models on various regions being connected via boundary models, a complex simulation domain may contain lots of different PDE systems to be solved. This may cause an extremely big global stiffness matrix and may exhaust performance and memory. To improve the behavior of the total system an equation system analyzer has been developed. Its duty is to check the different models applied to the simulation domains and the boundaries and interfaces for direct or indirect mutual dependencies. A direct dependence is meant to be a definite coupling between several solution quantities defined in a PDE system whereas an indirect dependence evolves from interface conditions stipulated by the simulation domain. If the analyzer detects independent quantities they are spread over different global stiffness matrices with the advantage to minimize memory usage as well as calculation time. Although theoretically there is no difference between solving two independent quantities at once and calculating each of them sequentially, it is a fact that the convergence of the linear solver is superior in case of smaller matrices since error propagation can be kept to smaller limits.
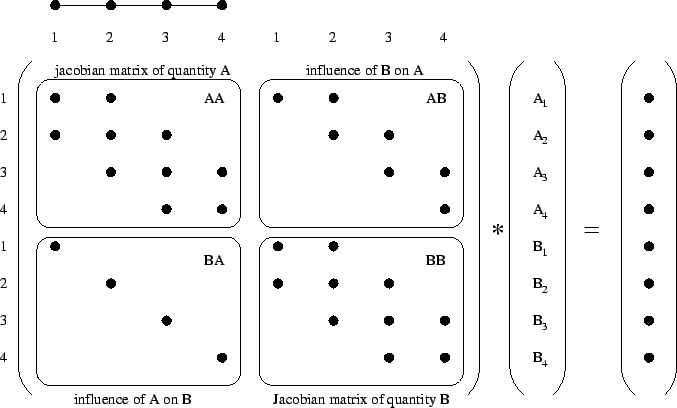
As an illustrative example the direct dependencies of a one-dimensional linear element with two points will be explained. A model with two coupled quantities (A,B) will be mapped on the discretized area, and the resulting matrix will be extracted.
AMI calculates the residual and its derivative, the Jacobian matrix, given by the model developer. The size and arrangement of the discretized quantities can be seen in Fig. 4.12.
The Jacobian matrix AA represents the discretized values on the element points for quantity A, and the same goes for quantity B describing the influence of the quantities itself on the corresponding result. The coupling submatrices AB and BA represent the influence of quantity A on B and vice versa. These terms decide whether the two quantities depend on each other (AB < > 0 or BA < > 0) or can be calculated independently (AB = 0 and BA = 0) in different global matrix systems.