5.1.4 Visco-Elastic Model

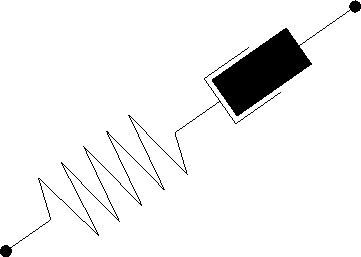
A more realistic approach to model the oxide and nitride layer is the assumption of a visco-elastic compressible fluid. In this case the stress is calculated from both the strain and the strain rate. The commonly used Maxwell body (Fig. 5.1) for the description of this phenomenon is analogous to a spring and a dashpot in series. The shape of the oxide is influenced by the history of the sample. This model must also be solved self consistently because of the close coupling.

Figure 5.1: Maxwell body: spring and a dashpot in series

The model is based on the idea that the dilatational components of the stress which involves the volumetric expansion, respectively compression, and the deviatoric part which only accounts for shape modifications, are decoupled. Thus, Hook's law can be written as

$$\left[\vphantom{ \begin{array}{c} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{zz}\\ \sigma _{xy}\\ \sigma _{yz}\\ \sigma _{zx} \end{array}}\right. \begin{array}{c} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{zz}\\ \sigma _{xy}\\ \sigma _{yz}\\ \sigma _{zx} \end{array} \left.\vphantom{ \begin{array}{c} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{zz}\\ \sigma _{xy}\\ \sigma _{yz}\\ \sigma _{zx} \end{array}}\right] \left(\vphantom{\chi\!\left [\begin{array}{cccccc} 1 & 1 & 1 & 0 ... ...0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] }\right. \chi \left[\vphantom{\begin{array}{cccccc} 1 & 1 & 1 & 0 & 0 & 0\\ 1 ... ...0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}}\right. \begin{array}{cccccc} 1 & 1 & 1 & 0 & 0 & 0\\ 1 & 1 & 1 & 0 & 0 ... ...0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \left.\vphantom{\begin{array}{cccccc} 1 & 1 & 1 & 0 & 0 & 0\\ 1 ... ...0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}}\right] \left[\vphantom{ \begin{array}{cccccc} \frac{4}{3} & -\frac{2}{3}... ...1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{array}}\right. \begin{array}{cccccc} \frac{4}{3} & -\frac{2}{3} & -\frac{2}{3} &... ...0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{array} \left.\vphantom{ \begin{array}{cccccc} \frac{4}{3} & -\frac{2}{3}... ...1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{array}}\right] \left.\vphantom{\chi\!\left [\begin{array}{cccccc} 1 & 1 & 1 & 0 ... ...0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] }\right) \left[\vphantom{ \begin{array}{c} \varepsilon _{xx}\\ \varepsilo... ...\varepsilon _{xy}\\ \varepsilon _{yz}\\ \varepsilon _{zx} \end{array}}\right. \begin{array}{c} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varep... ...{zz}\\ \varepsilon _{xy}\\ \varepsilon _{yz}\\ \varepsilon _{zx} \end{array} \left.\vphantom{ \begin{array}{c} \varepsilon _{xx}\\ \varepsilo... ...\varepsilon _{xy}\\ \varepsilon _{yz}\\ \varepsilon _{zx} \end{array}}\right]$$ (5.15)

where $\chi$ and G are the compressibility and modulus of rigidity of the body, respectively, which depend on the Young Modulus E and the Poisson ratio $\nu$.

The temporal evolution of the deviatoric components can directly be written as follows [Sen96]:

$$\sigma {\frac{\tau}{\Delta T}} \left(\vphantom{1-e^{\left(-\frac{\Delta T}{\tau_r}\right)}}\right. \left(\vphantom{-\frac{\Delta T}{\tau_r}}\right. {\frac{\Delta T}{\tau_r}} \left.\vphantom{-\frac{\Delta T}{\tau_r}}\right) \left.\vphantom{1-e^{\left(-\frac{\Delta T}{\tau_r}\right)}}\right) \varepsilon \varepsilon$$ (5.16)

with G_eff as an effective modulus of rigidity depending on the time period $\Delta$T of temporal discretization and $\tau_{r}^{}$ as the relaxation time. (5.16) is valid in case of short time periods $\Delta$T where the strain velocity can be kept constant.

Indeed, the deviatoric part of Maxwell fluid can be written as

$${\frac{d\varepsilon}{dt}} \left(\vphantom{\frac{1}{G}\cdot \frac{d\sigma}{dt} + \frac{1}{\eta}\cdot \sigma}\right. {\frac{1}{G}} {\frac{d\sigma}{dt}} {\frac{1}{\eta}} \sigma \left.\vphantom{\frac{1}{G}\cdot \frac{d\sigma}{dt} + \frac{1}{\eta}\cdot \sigma}\right)$$ (5.17)

The analytical solution of this equation gives the temporal evolution of the stress as a function of the strain velocity:

$$\sigma \sigma_{0}^{} {\frac{t-t_o}{\tau_r}} \int_{t_0}^{t} {\frac{t-\tau}{\tau_r}} {\frac{d\varepsilon}{dt}} \tau$$ (5.18)

with $\sigma_{0}^{}$ as the initial stress at time t₀.