| (4.3) |
| (4.3) |
Then the ratio of the estimated step size
![]()
![]() and the previous
step size
and the previous
step size
![]() tn is limited to the sectio aurea constant
(
tn is limited to the sectio aurea constant
(
![]() = 1.618...), to limit the step size
variations. With this restriction a quasi-uniform mesh is achieved, which
gives a second order local truncation error.
= 1.618...), to limit the step size
variations. With this restriction a quasi-uniform mesh is achieved, which
gives a second order local truncation error.
| (4.4) |
In order to follow the pointwise predefined input signals accurately it is necessary to calculate a time step at the instances used to specify the input signals. Therefore the step size has to be reduced if it is larger than the difference of the instance tk and the present time tn (see Fig. 4.7).
| (4.5) |
To avoid strong step size variations when reaching the next instance tk a
check is performed whether double the estimated step size is greater than the
difference of the instance tk and the actual time tn. In this case
the next two step sizes
![]()
![]() and
and
![]()
![]() are chosen in
such a way that the second step matches the instance and the step size ratio is
the sectio aurea constant (see Fig. 4.8).
are chosen in
such a way that the second step matches the instance and the step size ratio is
the sectio aurea constant (see Fig. 4.8).
| (4.6) | |
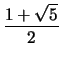 |
(4.7) |
|
Finally there is a check whether the estimated step size
![]()
![]() is
greater than a specified minimum step size
is
greater than a specified minimum step size
![]() tmin and less than a
specified maximum step size
tmin and less than a
specified maximum step size
![]() tmax.
tmax.
| (4.8) | ||
| (4.9) |