


Next: 4.6 Lösung des Gleichungssystems
Up: 4. Diskretisierung mit Finiten
Previous: 4.4 Elementformulierung
Unterabschnitte
Nachdem nun die einzelnen Integralterme der Gleichungen des Galerkin Ansatzes
elementweise bestimmt wurden, sollen nun die
Beiträge der Elemente aufsummiert werden, um das
Integral über das gesamte Gebiet 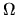 sowie den Rand
sowie den Rand 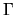 zu
bilden.
Daraus kann ein Gleichungssystem für die unbekannten
zu
bilden.
Daraus kann ein Gleichungssystem für die unbekannten 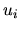 aufgestellt werden.
aufgestellt werden.
Das Gleichungssystem (4.28) kann in Matrixschreibweise angegeben werden
![$\displaystyle [A]\{\varphi\}=\{b\}\;.$](img309.png) |
(4.64) |
Dazu berechnet man zunächst die einzelnen Elementmatrizen mittels
(4.53) und (4.56), wobei für den Tensor
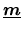 die
Permittivität
die
Permittivität
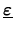 eingesetzt wird.
Die Matrix
eingesetzt wird.
Die Matrix ![$ [A]$](img310.png) wird dann durch Summierung über alle Elementmatrizen
gebildet
wird dann durch Summierung über alle Elementmatrizen
gebildet
![$\displaystyle [A]=\sum_{m=1}^M [A^{e_m}_L]\;.$](img311.png) |
(4.65) |
Diese Gleichung ist allerdings nur symbolisch zu verstehen.
Bei dieser Summierung wird nämlich
von der lokalen Knotennummerierung auf die globale übergegangen.
Hat beispielsweise der erste Knoten eines Elements den
globalen Index 17 und der zweite den Index 62, so bedeutet dies, dass
das Element (1,2) der Matrix
![$ [A^{e_m}_L]$](img312.png) an der Position (17,62)
in der Matrix
an der Position (17,62)
in der Matrix ![$ [A]$](img310.png) addiert wird.
Dieser Vorgang wird als Assemblierung bezeichnet.
addiert wird.
Dieser Vorgang wird als Assemblierung bezeichnet.
Gleichermaßen geht man
bei der Summierung der Randterme
von lokaler auf globale Knotennummerierung über
Die Spaltenmatrix 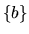 ergibt sich als Summe der
Beiträge der Elemente am Rand
des Simulationsgebietes, kann also nur für Randknoten einen Wert ungleich
Null haben. Genauer gesagt, tritt eine Flächenladung
ergibt sich als Summe der
Beiträge der Elemente am Rand
des Simulationsgebietes, kann also nur für Randknoten einen Wert ungleich
Null haben. Genauer gesagt, tritt eine Flächenladung 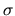 nur an den
Elektroden auf--das sind jene Knoten, die eine Dirichlet-Randbedingung
haben.
Deshalb können auch nur an diesen Stellen des
nur an den
Elektroden auf--das sind jene Knoten, die eine Dirichlet-Randbedingung
haben.
Deshalb können auch nur an diesen Stellen des 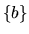 -Vektors
Einträge ungleich Null vorhanden sein.
Das Gleichungssystem (4.64) kann auch detailliert angeschrieben
werden, wobei die obere Hälfte des Gleichungssystems den inneren Knoten
und die untere Hälfte den Randknoten auf
-Vektors
Einträge ungleich Null vorhanden sein.
Das Gleichungssystem (4.64) kann auch detailliert angeschrieben
werden, wobei die obere Hälfte des Gleichungssystems den inneren Knoten
und die untere Hälfte den Randknoten auf 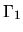 zugeordnet ist
(die unbekannten Werte sind unterstrichen):
zugeordnet ist
(die unbekannten Werte sind unterstrichen):
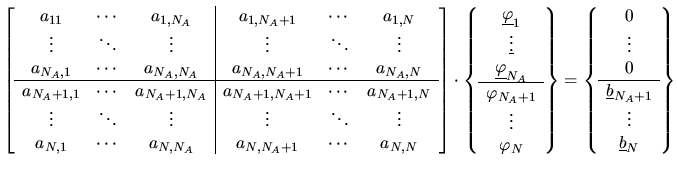 |
(4.67) |
oder als Teilmatrizen dargestellt
![$\displaystyle \begin{bmatrix}[A_A]\phantom{{}^T} & [A_B] \\ {} [A_B]^T & [A_D]...
...ay}\right\}=\left\{\begin{array}{c} \{0\} \\ \{ b_D \} \\ \end{array}\right\}$](img316.png) |
(4.68) |
Um nun die unbekannten Potenzialwerte
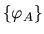 im Inneren des
Leiters zu erhalten, muss man das folgende Gleichungssystem lösen:
im Inneren des
Leiters zu erhalten, muss man das folgende Gleichungssystem lösen:
![$\displaystyle [A_A]\cdot\{\varphi_A\}=-[A_B]\cdot\{\varphi_D\}$](img318.png) |
(4.69) |
auf den Elektroden werden berechnet, indem man
die Spaltenmatrix 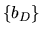 mit der folgenden Gleichung ermittelt:
mit der folgenden Gleichung ermittelt:
![$\displaystyle \{b_D\}=[A_B]^T\cdot\{\varphi_A\}+[A_D]\cdot\{\varphi_D\}$](img320.png) |
(4.70) |
und dann das Gleichungssystem
![$\displaystyle [B]\{\sigma\}=\{b\}$](img321.png) |
(4.71) |
löst.
Die Matrix ![$ [B]$](img322.png) setzt sich aus den Elementmatrizen der Randelemente, die an
den Oberflächen der Elektroden liegen, zusammen:
setzt sich aus den Elementmatrizen der Randelemente, die an
den Oberflächen der Elektroden liegen, zusammen:
![$\displaystyle [B]=\sum_{m=1}^{M_B} [A^{e_m}_B] \,.$](img323.png) |
(4.72) |
Bei der Summierung muss wieder von der lokalen Knotennummerierung der
Elementmatrizen
![$ [A^{e_m}_B]$](img324.png) auf die globale Nummerierung übergegangen
werden.
Nummeriert man die Gitterknoten in einer Reihenfolge, sodass Knoten auf gleichen
Elektroden durchlaufende Indizes haben, dann ergibt sich für die Matrix
auf die globale Nummerierung übergegangen
werden.
Nummeriert man die Gitterknoten in einer Reihenfolge, sodass Knoten auf gleichen
Elektroden durchlaufende Indizes haben, dann ergibt sich für die Matrix
![$ [B]$](img322.png) eine Blockstruktur.
eine Blockstruktur.
![$\displaystyle \begin{bmatrix}[0]& [0] & [0] & [0] \\ {} [0] & [B_1] & [0] & [0...
...\{\begin{array}{c} \{0\} \\ \{b_1\} \\ \vdots \\ \{b_n\} \end{array}\right\}$](img325.png) |
(4.73) |
Jeder der 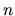 Blöcke kann einer Elektrode zugeordnet werden, und das
Gleichungssystem kann nach Elektroden separiert gelöst werden.
Blöcke kann einer Elektrode zugeordnet werden, und das
Gleichungssystem kann nach Elektroden separiert gelöst werden.
erfordern eine spezielle Behandlung,
da hier weder das Potenzial der Elektrode noch die Verteilung der Ladung
bzw. die entsprechenden Einträge im 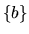 -Vektor bekannt sind.
Im Folgenden wird angenommen, die Knoten mit den globalen
Indizes
-Vektor bekannt sind.
Im Folgenden wird angenommen, die Knoten mit den globalen
Indizes  seien Randknoten einer schwebenden Elektrode.
Dann folgt aus (2.20) unmittelbar
seien Randknoten einer schwebenden Elektrode.
Dann folgt aus (2.20) unmittelbar
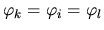 für für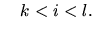 |
(4.74) |
Aus (4.61) sowie (4.48) lässt sich zeigen
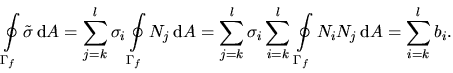 |
(4.75) |
Aus (2.21) resultiert somit die Forderung
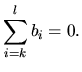 |
(4.76) |
Bei der Lösung des Gleichungssystems müssen nun (4.74) und
(4.76) als zusätzliche Gleichungen in das System aufgenommen werden,
oder man nutzt (4.74) um die Gleichungen 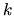 bis
bis 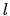 zu eliminieren.
Dazu ersetzt man in der Matrix
zu eliminieren.
Dazu ersetzt man in der Matrix ![$ [A]$](img310.png) die Zeilen
die Zeilen 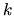 bis
bis 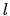 durch eine einzelne
Zeile mit den Spaltensummen der eliminierten Zeilen.
Dasselbe wird natürlich auch für die Spalten von
durch eine einzelne
Zeile mit den Spaltensummen der eliminierten Zeilen.
Dasselbe wird natürlich auch für die Spalten von ![$ [A]$](img310.png) durchgeführt.
Beim
durchgeführt.
Beim 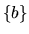 -Vektor werden ebenfalls die Zeilen
-Vektor werden ebenfalls die Zeilen 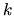 bis
bis 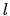 entfernt und durch
eine einzelne Null ersetzt.
entfernt und durch
eine einzelne Null ersetzt.
kann mittels
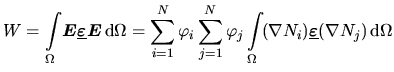 |
(4.77) |
berechnet werden und ergibt
![$\displaystyle W=\frac12\{\varphi\}^T[A]\{\varphi\}=\frac12\{\varphi\}^T\{b\} =\frac12\{\varphi_D\}^T\{b_D\}\;.$](img332.png) |
(4.78) |
Nimmt man wieder an, dass die Knoten, die zu einer Elektrode gehören,
fortlaufend nummeriert sind so kann obige Gleichung in Teilsummen, die den
einzelnen Elektroden zugeordnet sind, gegliedert werden
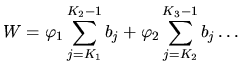 |
(4.79) |
Die Potenzialwerte
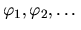 sind auf den Elektroden
konstant und wurden deshalb vor die Summe gehoben.
Die Summierung über die
sind auf den Elektroden
konstant und wurden deshalb vor die Summe gehoben.
Die Summierung über die 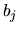 entspricht gemäß (4.75) der Ladung
auf der jeweiligen Elektrode.
Die Energie des Feldes entspricht deshalb der Summe der Produkte aus Ladung
und Potenzial der einzelnen Elektroden.
Für die Kapazitätsberechnung mit Finiten Elementen bedeutet dies,
dass die Methode der
Ladungsintegration und die Energiemethode völlig äquivalent sind.
entspricht gemäß (4.75) der Ladung
auf der jeweiligen Elektrode.
Die Energie des Feldes entspricht deshalb der Summe der Produkte aus Ladung
und Potenzial der einzelnen Elektroden.
Für die Kapazitätsberechnung mit Finiten Elementen bedeutet dies,
dass die Methode der
Ladungsintegration und die Energiemethode völlig äquivalent sind.
Die Berechnung der Potenzialverteilung und Stromdichte in elektrischen
Leitern kann analog zur Berechnung des Elektrischen Feldes in
dielektrischen Materialien erfolgen.
Man erhält wieder ein Gleichungssystem der Form
![$\displaystyle [A]\{\varphi\}=\{b\}$](img336.png) |
(4.80) |
mit
Die Berechnung der Elementmatrizen
![$ [A^{e_m}_L]$](img312.png) erfolgt mit (4.56)
und (4.54), wobei für den Materialfaktor
erfolgt mit (4.56)
und (4.54), wobei für den Materialfaktor
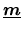 die elektrische
Leitfähigkeit
die elektrische
Leitfähigkeit 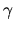 eingesetzt wird.
In (4.81) und (4.82) wird wieder bei der Summenbildung von
lokalen auf globale Knotennummerierung übergewechselt.
Die Matrix
eingesetzt wird.
In (4.81) und (4.82) wird wieder bei der Summenbildung von
lokalen auf globale Knotennummerierung übergewechselt.
Die Matrix ![$ [A]$](img310.png) kann äquivalent zu (4.68) in die Teilmatrizen
kann äquivalent zu (4.68) in die Teilmatrizen
![$ [A_A]$](img339.png) ,
, ![$ [A_B]$](img340.png) ,
, ![$ [A_B]^T$](img341.png) und
und ![$ [A_D]$](img342.png) aufgeteilt werden.
Auch die Spaltenmatrix
aufgeteilt werden.
Auch die Spaltenmatrix 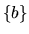 wird aufgeteilt in
wird aufgeteilt in
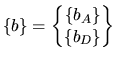 |
(4.83) |
zeichnen sich dadurch aus, dass
in der Spaltenmatrix 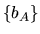 , die den entsprechenden Randknoten zuordenbare Zeilen,
von Null verschiedene Einträge haben.
, die den entsprechenden Randknoten zuordenbare Zeilen,
von Null verschiedene Einträge haben.
Die unbekannten Potenzialwerte
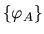 erhält man nun durch Lösen
des Gleichungssystems
erhält man nun durch Lösen
des Gleichungssystems
![$\displaystyle [A_A]\{\varphi_A\}=\{b_A\}-[A_B]\{\varphi_D\}.$](img345.png) |
(4.84) |
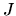 auf Dirichlet'schen Rändern kann mit
(4.70) bis (4.73) berechnet werden, indem formal
auf Dirichlet'schen Rändern kann mit
(4.70) bis (4.73) berechnet werden, indem formal 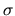 durch
durch
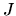 ersetzt wird.
ersetzt wird.
gilt für das Potenzial (4.74) und für den Gesamtstrom in Analogie zu
(4.76)
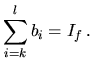 |
(4.85) |
Diese Bedingungen können, wie zuvor bei der Berechnung des
elektrostatischen Feldes, in das Gleichungssystem eingebaut werden, indem man
die entsprechenden Zeilen und Spalten zusammenfasst.
ergibt sich als
![$\displaystyle W=\{\varphi\}^T[A]\{\varphi\}=\{\varphi\}^T\{b\}$](img348.png) |
(4.86) |
Gleichung 4.37 kann in Matrixschreibweise in folgendermaßen
angeschrieben werden:
![$\displaystyle [M_1]\{\dot\varphi\}=-[M_2]\{\varphi\}+[M_3]\{J\}.$](img349.png) |
(4.87) |
wird vorgenommen, indem man eine Integration
über einen Zeitschritt
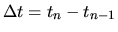 durchführt.
(Zwecks Abkürzung wird für das Potenzial
durchführt.
(Zwecks Abkürzung wird für das Potenzial
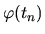 zum Zeitschritt
zum Zeitschritt 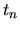 einfach
einfach 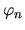 geschrieben.)
geschrieben.)
![$\displaystyle [M_1]\bigl(\{\varphi_n\}-\{\varphi_{n-1}\}\bigr)= -[M_2]\int_{t_{...
...{t_n}\!\{\varphi\}\,\textrm{d}t + [M_3]\int_{t_{n-1}}^{t_n}\!\{J\}\,\textrm{d}t$](img354.png) |
(4.88) |
Zur Lösung dieser Integrale sollen nun zwei verschiedene Näherungsverfahren
betrachtet werden, nämlich das Rückwärts-Euler-Verfahren,
das sich durch numerische Stabilität auszeichnet und die
Trapezmethode, (oft auch als Crank-Nicolson-Verfahren bezeichnet)
mit der im Allgemeinen eine höhere Genauigkeit erreicht werden kann.
Beim Rückwärts-Euler-Verfahren wird das Integral über einen Zeitschritt
durch die Fläche eines Rechtecks angenähert
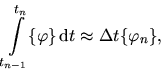 |
(4.89) |
bei der Trapezmethode hingegen durch die Fläche eines Trapezes
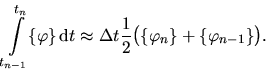 |
(4.90) |
Setzt man nun eine der beiden Näherungsformeln in (4.88) ein, erhält
man wiederum ein Gleichungssystem der Form
![$\displaystyle [A]\{\varphi_n\}=\{b\}$](img357.png) |
(4.91) |
mit
![$\displaystyle \{b\}=[\bar A]\{\varphi_{n-1}\}+[B]\int_{t_{n-1}}^{t_n}\!\{J\}\,\textrm{d}t$](img358.png) |
(4.92) |
mit dem man
das Potenzial zum aktuellen Zeitpunkt 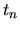 ausgehend vom Potenzial zum vorhergegangenem Zeitpunkt
ausgehend vom Potenzial zum vorhergegangenem Zeitpunkt 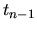 berechnen kann.
Dabei beginnt man zum Zeitpunkt
berechnen kann.
Dabei beginnt man zum Zeitpunkt 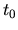 mit dem Potenzial
mit dem Potenzial
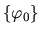 laut Anfangsbedingung (2.41).
laut Anfangsbedingung (2.41).
Für die Diskretisierung mittels Rückwärts-Euler-Verfahren gilt
Bei der Trapezmethode gilt
In beiden Fällen erhält man die Matrix ![$ [B]$](img322.png) durch Summierung über alle
Randelemente mit inhomogenen Neumann-Bedingungen
durch Summierung über alle
Randelemente mit inhomogenen Neumann-Bedingungen
![$\displaystyle [B]=[M_3]=\sum_{m=1}^M [A^{e_m}_B].$](img368.png) |
(4.97) |
Die Summenformeln in (4.93) bis (4.97) sind hier wieder nur
symbolisch zu verstehen, da während der Summierung von der lokalen zur
globalen Knotennummerierung gewechselt wird.
Die Matrix ![$ [A]$](img310.png) kann wieder, wie in (4.68), in die Teilmatrizen
kann wieder, wie in (4.68), in die Teilmatrizen
![$ [A_A]$](img339.png) ,
, ![$ [A_B]$](img340.png) ,
, ![$ [A_B]^T$](img341.png) und
und ![$ [A_D]$](img342.png) aufgeteilt werden, ebenso die
Spaltenmatrix
aufgeteilt werden, ebenso die
Spaltenmatrix 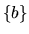 , wie in (4.83).
Damit kann man die unbekannten Potenzialwerte
, wie in (4.83).
Damit kann man die unbekannten Potenzialwerte
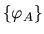 wie
in (4.84) berechnen.
wie
in (4.84) berechnen.
Das Gleichungssystem zur Berechnung der stationären Temperaturverteilung
(4.39) kann in Matrixschreibweise als
![$\displaystyle [A]\{T\}=\{b\}$](img369.png) |
(4.98) |
angeschrieben werden mit
![$\displaystyle [A]=\sum_{m=1}^M [A^{e_m}_{L,\gamma_T}]$](img370.png) |
(4.99) |
und
![$\displaystyle \{b\}=\sum_{m=1}^M [A^{e_m}_P] \{p\} +\sum_{m=1}^M [A^{e_m}_B]\{\Theta\}\,.$](img371.png) |
(4.100) |
Beim Bilden der Summen wird hier wieder von lokaler auf globale
Knotennummerierung übergegangen.
Wählt man die Reihenfolge der Einträge der Spaltenmatrix der Temperatur
wieder so, dass
Knoten mit Dirichlet-Bedingungen am Schluss aufscheinen, kann man
die Gleichung wie in (4.68) aufspalten und man erhält die
unbekannten Temperaturwerte 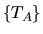 als Lösung des folgenden
Gleichungssystems:
als Lösung des folgenden
Gleichungssystems:
![$\displaystyle [A_A]\{T_A\}=\{b_A\}-[A_B]\{T_D\} \,.$](img373.png) |
(4.101) |
Gleichung 4.40 hat die Form
![$\displaystyle [M_1]\{\dot T\}=-[M_2]\{T\}+[M_3]\{p\}+[M_4]\{\Theta\}$](img374.png) |
(4.102) |
Die Zeitdiskretisierung wird äquivalent zu (4.88)-(4.90)
mit dem Rückwärts-Euler- oder Trapezverfahren vorgenommen.
Man erhält wiederum ein Gleichungssystem der Form
![$\displaystyle [A]\{T_n\}=\{b\}$](img375.png) |
(4.103) |
mit
![$\displaystyle \{b\}=[\bar A]\{T_{n-1}\} +\sum_{m=1}^M [A^{e_m}_P]\int_{t_n}^{t_...
...{d}t +\sum_{m=1}^M [A^{e_m}_B]\int_{t_n}^{t_{n-1}}\!\{\theta\}\,\textrm{d}t \,.$](img376.png) |
(4.104) |
Beim Rückwärts-Euler-Verfahren erhält man die
Matrizen ![$ [A]$](img310.png) und
und ![$ [\bar A]$](img377.png) mit
mit
und beim Trapezverfahren mit
Im Fall, dass der thermische Leitwert 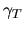 oder die
Wärmekapazität
oder die
Wärmekapazität 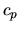 einzelner Materialien nicht
konstant ist, muss das natürlich bei der Assemblierung der Matrizen
einzelner Materialien nicht
konstant ist, muss das natürlich bei der Assemblierung der Matrizen ![$ [A]$](img310.png) und
und ![$ [\bar A]$](img377.png) berücksichtigt werden. Und zwar müssen für
berücksichtigt werden. Und zwar müssen für ![$ [A]$](img310.png) die
Werte zum Zeitpunkt
die
Werte zum Zeitpunkt 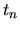 und für
und für ![$ [\bar A]$](img377.png) zum Zeitpunkt
zum Zeitpunkt 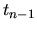 verwendet werden.
verwendet werden.
Da die elektrischen Zeitkonstanten in der Regel sehr viel kürzer sind als
die thermischen, wird für die Berechnung des elektrischen Systems eine
stationäre Stromverteilung angenommen. Unter der Voraussetzung, dass die
elektrischen Parameter keine Temperaturabhängigkeit aufweisen, ist deshalb
auch die Verlustleistungsdichte 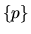 konstant und das Integral aus
(4.104) vereinfacht sich zu
konstant und das Integral aus
(4.104) vereinfacht sich zu
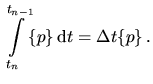 |
(4.109) |
Ist hingegen etwa die elektrische Leitfähigkeit von der Temperatur abhängig,
muss zur Bestimmung der Verlustleistungsdichte das elektrische System für
jeden Zeitschritt neu berechnet werden und das Integral aus (4.104)
kann mittels der Trapezformel genähert werden
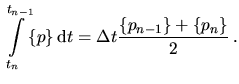 |
(4.110) |
Gleichung 4.103 kann dann wieder, wie in (4.68), aufgespalten
werden und man erhält die unbekannten Temperaturwerte 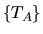 als
Lösung des Gleichungssystems (4.101).
als
Lösung des Gleichungssystems (4.101).



Next: 4.6 Lösung des Gleichungssystems
Up: 4. Diskretisierung mit Finiten
Previous: 4.4 Elementformulierung
R. Sabelka: Dreidimensionale Finite Elemente Simulation von Verdrahtungsstrukturen auf Integrierten Schaltungen
![]() sowie den Rand
sowie den Rand ![]() zu
bilden.
Daraus kann ein Gleichungssystem für die unbekannten
zu
bilden.
Daraus kann ein Gleichungssystem für die unbekannten ![]() aufgestellt werden.
aufgestellt werden.
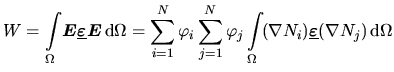
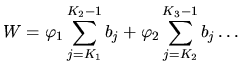
![]() erhält man nun durch Lösen
des Gleichungssystems
erhält man nun durch Lösen
des Gleichungssystems
![]() kann wieder, wie in (4.68), in die Teilmatrizen
kann wieder, wie in (4.68), in die Teilmatrizen
![]() ,
, ![]() ,
, ![]() und
und ![]() aufgeteilt werden, ebenso die
Spaltenmatrix
aufgeteilt werden, ebenso die
Spaltenmatrix ![]() , wie in (4.83).
Damit kann man die unbekannten Potenzialwerte
, wie in (4.83).
Damit kann man die unbekannten Potenzialwerte
![]() wie
in (4.84) berechnen.
wie
in (4.84) berechnen.
![]() als Lösung des folgenden
Gleichungssystems:
als Lösung des folgenden
Gleichungssystems:
![]() konstant und das Integral aus
(4.104) vereinfacht sich zu
konstant und das Integral aus
(4.104) vereinfacht sich zu