Zur Lösung des nichtlinearen Gleichungssystems
wird mittels Newton-Verfahren eine Folge von Näherungslösungen
berechnet, deren Grenzwert die gesuchte Lösung
ist,
Betrachtet man die Taylor-Reihenentwicklung
so findet man, daß für
, also für den
Fall, daß 
linear ist, mit der Berechnung des
linearen Gleichungssystems
und
die Lösung bestimmt werden kann. Ist
nichtlinear, so ist jedoch
und der Vorgang muß solange wiederholt werden, bis ein Näherungswert
für die Lösung mit der gewünschten Genauigkeit berechnet ist. Die
Matrix 
ist die
Systemmatrix (Jacobi-Matrix) oder die Ableitung von
.
Der Startwert 
muß nahe genug der Lösung gewählt
werden, damit das Newton-Verfahren konvergiert,
Eine quantitative Aussage über 
ist jedoch nicht
möglich, sodaß für die Wahl von Erfahrungswerte
verwendet werden müssen. Für MINIMOS-NT werden folgende Startwerte
verwendet [11]:
Es zeigt sich, daß durch das Verfahren nach Newton mit der Berechnung
des Inkrementvektors 
der Betrag der Korrektur für
einen bestimmten Wert der Folge 
überschätzt wird. Das
hat zur Folge, daß mitunter der Konvergenzbereich
verlassen wird und das
Newton-Verfahren divergiert. Das kann durch Dämpfung des
Inkrementvektors vermieden werden,
Für die Berechnung des Dämpfungsfaktors 
gibt es
verschiedene Strategien. Für MINIMOS-NT hat sich eine Strategie
bewährt, welche den Betrag des Inkrementvektors logarithmisch
begrenzt [11]:
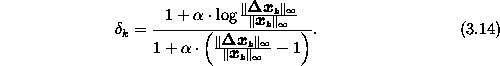
Je größer 
gewählt wird, umso mehr kommt die logarithmische
Dämpfung zum Tragen. Für 
wird entweder der gesamte
Inkrement-, bzw. Lösungsvektor verwendet (Gesamtnorm) oder nur der
Teil, der das elektrostatische Potential enthält (Potentialnorm)
(siehe unten).
Für Simulationen, die das Drift-Diffusionsmodell verwenden, gewährleistet die Dämpfung mit der Potentialnorm in den meisten Fällen die Konvergenz des modifizierten Newton-Verfahrens. Schwieriger gestaltet sich die Situation im Falle der Simulation mit dem hydrodynamischen Modell.
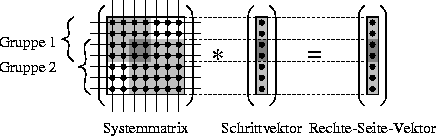
Abbildung 3.4: Für Simulationen, die das hydrodynamische
Modell verwenden, kommt ein blockiteratives Verfahren zur Anwendung.
Die Gleichungen werden zu Gruppen zusammengefaßt und gruppenweise
gelöst. Damit werden zum einen Kopplungen unterdrückt, welche die
Richtung und die Länge des Inkrementvektors negativ beeinflussen. Zum
anderen werden alte und neue Teile des Lösungsvektors kombiniert.
Beides bewirkt eine gleichmäßigere Konvergenz.
Aufgrund der geringen Wärmekapazität des Ladungsträgergases sind die Ladungsträgertemperaturen von Iterationsschritt zu Iterationsschritt starken Schwankungen unterworfen. Sind die Ladungsträgertemperaturen für den gewählten Arbeitspunkt hoch, verhindern diese Schwankungen eine Konvergenz des Newton-Verfahrens.
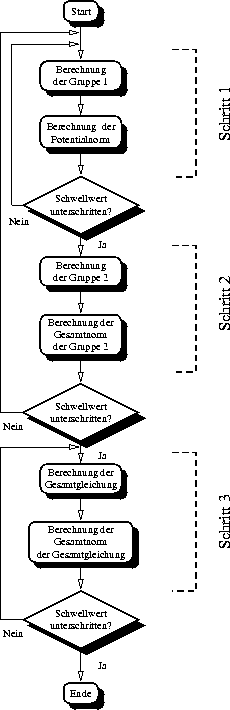
Abbildung 3.5: Ablaufschema des
blockiterativen Lösungsvorgangs für hydrodynamische Simulationen. In
Schritt 1 werden die Poisson-Gleichung und die beiden
Kontinuitätsgleichungen gelöst, in Schritt 2 die beiden
Kontinuitätsgleichungen und die beiden Energietransportgleichungen
und in Schritt 3 alle fünf Gleichungen gemeinsam.
Abhilfe schafft hier ein blockiteratives Verfahren. Dazu werden die Gleichungen des linearen Systems zu Gruppen zusammengefaßt. Die in Abbildung 3.4 gezeigte Gruppe 1 enthält die Poissongleichung und die beiden Kontinuitätsgleichungen. Gruppe 2 besteht aus den beiden Kontinuitätsgleichungen und den beiden Energietransportgleichungen. Abbildung 3.5 zeigt in welcher Reihenfolge die Gruppen gelöst werden. Gruppe 1 wird in einer eigenen Iterationsschleife gelöst, bis die Potentialnorm des Inkrementvektors einen temporären Schwellwert unterschritten hat. Dann wird einmal Gruppe 2 gelöst. Diese beiden Schritte werden in einer äußeren Schleife solange fortgesetzt, bis sowohl die Potentialnorm von Schritt 1 als auch die Gesamtnorm von Schritt 2 ihren jeweiligen temporären Schwellwert unterschritten haben. Ist das der Fall, wird das gesamte Gleichungssystem gekoppelt gelöst, bis die Gesamtnorm des Inkrementvektors den entsprechenden Schwellwert unterschreitet. Dieses Verfahren erlaubt es, auch für Arbeitspunkte für die mit einer gekoppelte Lösung keine Konvergenz erzielt werden konnte eine Lösung zu finden.
Mit diesem Schema ist es auch möglich, bei der Simulation von Bauelementen, deren Ladungsträgerkonzentrationen schwierig zu berechnen sind, wie etwa die Löcherkonzentration in SOI-Bauelementen, und deren Systemmatrix daher eine schlechte Kondition aufweist, die Kontinuitätsgleichungen zu einer Gruppe zusammenzufassen und nach einem Gesamtschritt mit einigen Iterationen nur die nichtlinearen Kontinuitätsgleichungen zu berechnen um Konvergenz zu erzielen.
