Using (4.57) and the combined rejection technique developed for the secondary trajectories based on the inequalities (4.78) to
(4.80), the new small-signal Monte Carlo algorithm including the Pauli exclusion principle can be formulated as follows:
- Simulate the nonlinear Boltzmann equation until
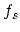 has converged.
has converged.
- Follow a main trajectory for one free flight. Store the before-scattering state in
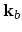 , and realize a scattering
event from
, and realize a scattering
event from
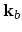 to
to
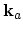 .
.
- Start a trajectory
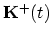 from
from
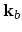 and another trajectory
and another trajectory
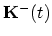 from
from
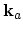 .
.
- Follow both trajectories for time
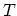 using the rejection scheme based on the acceptance conditions
(4.78) to (4.80). At equidistant times
using the rejection scheme based on the acceptance conditions
(4.78) to (4.80). At equidistant times 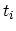 add
add
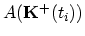 to a histogram
to a histogram
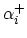 and
and
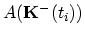 to a histogram
to a histogram
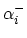 .
.
- Continue with the second step until
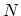
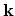 -points have been generated.
-points have been generated.
- Calculate the time discrete impulse response as
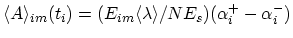 .
.
This algorithm is schematically illustrated in Fig. 4.7 and its flow chart is shown in Fig. 4.8.
Figure 4.7:
Schematic representation of the small-signal algorithm.
|
|
It should be noted that in a highly degenerate electron gas the main trajectory contains many self-scattering events. As in this case
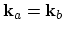 , the corresponding two secondary trajectories will give the same contribution, that is
, the corresponding two secondary trajectories will give the same contribution, that is
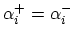 . This
does not change the impulse response. Thus in order to save the computation time it is reasonable not to start trajectories
. This
does not change the impulse response. Thus in order to save the computation time it is reasonable not to start trajectories 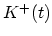 and
and 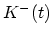 after a self-scattering event has occurred.
after a self-scattering event has occurred.
Figure 4.8:
Flow chart of the small-signal algorithm.
|
|
If a self-scattering event has taken place during the evolution of the main trajectory, the main trajectory is continued until a physical scattering event
has happened. Only at this moment the secondary trajectories 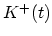 and
and 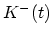 are started.
are started.
S. Smirnov: