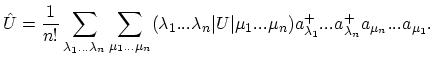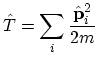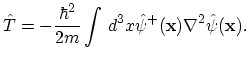For each single-particle state
 of the single-particle Hilbert space
of the single-particle Hilbert space
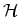 a Boson or Fermion creation operator
a Boson or Fermion creation operator
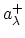 is defined by its action on any symmetrized or antisymmetrized state
is defined by its action on any symmetrized or antisymmetrized state
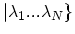 of the Hilbert space of
of the Hilbert space of 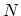 Bosons,
Bosons,
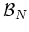 , or
, or 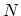 Fermions,
Fermions,
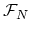 , as follows:
, as follows:
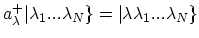 |
(A.4) |
The creation operators
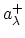 do not operate within one space
do not operate within one space
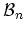 or
or
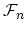 , but rather operate from any space
, but rather operate from any space
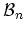 or
or
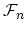 to
to
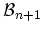 or
or
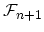 . It is useful to define the Fock space as the direct sum of the
Boson or Fermion spaces
. It is useful to define the Fock space as the direct sum of the
Boson or Fermion spaces
| |
|
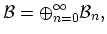 |
(A.5) |
| |
|
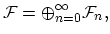 |
|
where by definition:
| |
|
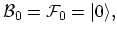 |
(A.6) |
| |
|
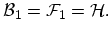 |
|
It can be easily shown that for Bosons the creation operators commute:
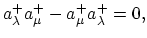 |
(A.7) |
whereas they anticommute for Fermions:
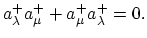 |
(A.8) |
The annihilation operators
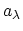 are defined as the adjoints of the creation operators
are defined as the adjoints of the creation operators
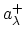 . The commutation and anticommutation
relations of annihilation operators follow from (A.7) and (A.8), respectively. They commute for Bosons:
. The commutation and anticommutation
relations of annihilation operators follow from (A.7) and (A.8), respectively. They commute for Bosons:
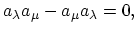 |
(A.9) |
whereas they anticommute for Fermions:
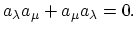 |
(A.10) |
The action of the annihilation operator on a many particle state is given for Bosons as
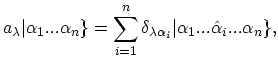 |
(A.11) |
while for Fermions it reads:
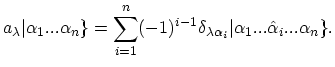 |
(A.12) |
Here
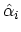 shows that the state
shows that the state
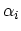 has been removed from the mani-particle state
has been removed from the mani-particle state
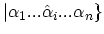 .
.
The commutation rules for the creation and annihilation operators are:
If the orthonormal basis
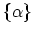 transforms into another basis
transforms into another basis
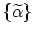 , the creation and annihilation operators transform as
follows:
, the creation and annihilation operators transform as
follows:
| |
|
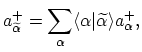 |
(A.14) |
| |
|
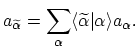 |
|
Of particular importance is the coordinate basis
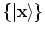 . In this case the creation and annihilation operators are traditionally denoted by
. In this case the creation and annihilation operators are traditionally denoted by
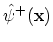 and
and
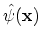 and are called field operators. From (A.15) it follows:
and are called field operators. From (A.15) it follows:
| |
|
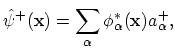 |
(A.15) |
| |
|
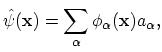 |
|
where
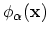 is the coordinate representation wave function of the state
is the coordinate representation wave function of the state
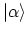 .
.
It can be shown that 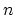 -body operators (A.3) can be expressed through the creation and annihilation operators in a simple form:
-body operators (A.3) can be expressed through the creation and annihilation operators in a simple form:
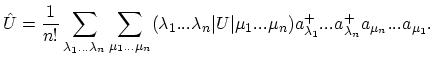 |
(A.16) |
For example using the coordinate representation, the kinetic energy operator 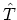
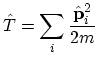 |
(A.17) |
may be rewritten in second quantized form as:
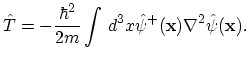 |
(A.18) |
S. Smirnov:
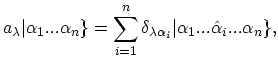
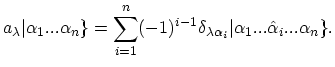
![]() transforms into another basis
transforms into another basis
![]() , the creation and annihilation operators transform as
follows:
, the creation and annihilation operators transform as
follows:
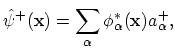
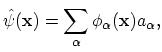
![]() -body operators (A.3) can be expressed through the creation and annihilation operators in a simple form:
-body operators (A.3) can be expressed through the creation and annihilation operators in a simple form: