The motion in real space is described by the following equation:
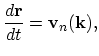 |
(2.7) |
where
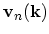 is the quantum mechanical average of the velocity operator over an electron state represented as a Bloch wave packet for band
index n:
is the quantum mechanical average of the velocity operator over an electron state represented as a Bloch wave packet for band
index n:
| |
|
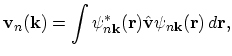 |
|
| |
|
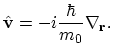 |
(2.8) |
Using Bloch's wave function with the periodic amplitude
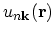 and the ortho-normality condition, equation (2.8) gives:
and the ortho-normality condition, equation (2.8) gives:
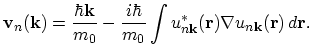 |
(2.9) |
The important difference of this expression from that of the free electron theory consists in the second term which is in general
not equal to zero. Thus
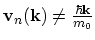 and the directions of the quantum mechanical average of the velocity and
quasi-momentum do not coincide in general as it is shown in Fig. 2.1.
and the directions of the quantum mechanical average of the velocity and
quasi-momentum do not coincide in general as it is shown in Fig. 2.1.
Figure:
Momentum and quasi-momentum differ by the vector
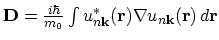 .
.
|
|
In the limiting case of free electrons the amplitude
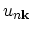 does not depend on position and thus the second term in (2.9) vanishes.
In this case
does not depend on position and thus the second term in (2.9) vanishes.
In this case
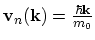 as in the
theory of free electrons. This is another consequence of the quantum mechanical aspect of the semiclassical model, which uses the concept of
quasi-momentum.
as in the
theory of free electrons. This is another consequence of the quantum mechanical aspect of the semiclassical model, which uses the concept of
quasi-momentum.
Note that the quasi-momentum does not coincide with the momentum of a Bloch electron. The point is that the momentum
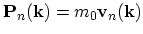 of an electron changes under the action of the total force which also includes the periodic potential.
The quasi-momentum
of an electron changes under the action of the total force which also includes the periodic potential.
The quasi-momentum
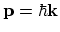 of an electron only changes under the action of external fields and the periodic field of a crystal does not
change the quasi-momentum of an electron.
of an electron only changes under the action of external fields and the periodic field of a crystal does not
change the quasi-momentum of an electron.
S. Smirnov:
![]() and the ortho-normality condition, equation (2.8) gives:
and the ortho-normality condition, equation (2.8) gives:
![]() of an electron changes under the action of the total force which also includes the periodic potential.
The quasi-momentum
of an electron changes under the action of the total force which also includes the periodic potential.
The quasi-momentum
![]() of an electron only changes under the action of external fields and the periodic field of a crystal does not
change the quasi-momentum of an electron.
of an electron only changes under the action of external fields and the periodic field of a crystal does not
change the quasi-momentum of an electron.