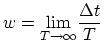Using the equations of motion described in Section 2.1 it is in principle possible to obtain the complete information about the motion
of particles in a solid. However, in practice it would be necessary to solve a huge number of ordinary differential equations, which is not possible from
a computational point of view. Due to the large number of degrees of freedom particle trajectories are on the one hand very quickly mixed in a complex way
such that there is no possibility to find some regularity in physical properties but on the other hand new properties come into play at large number of
degrees of freedom. These properties allow the system to be described by a statistical approach. This approach has nothing to do with mechanical
regularity of a system and does not make any sense for systems with a small number of particles.
The statistical approach considers a closed system. From this system a subsystem2.1 is separated, which is not closed and interacts with other subsystems of the system. Because of the large number of degrees of
freedom of the system the interactions have a very complex character. Thus the state of the subsystem changes in a complex way. By this very nature the
subsystem passes many times all its states during a rather long time interval 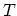 . A small domain2.2
. A small domain2.2
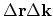 of the subsystem will be visited many times. If
of the subsystem will be visited many times. If 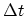 is the total time the subsystem spends in
is the total time the subsystem spends in
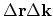 , the quantity
, the quantity
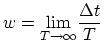 |
(2.20) |
can be treated as the probability of finding the subsystem in a state within the phase space domain
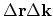 around
around
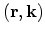 .
.
Subsections
S. Smirnov:
![]() . A small domain2.2
. A small domain2.2
![]() of the subsystem will be visited many times. If
of the subsystem will be visited many times. If ![]() is the total time the subsystem spends in
is the total time the subsystem spends in
![]() , the quantity
, the quantity