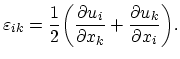Under applied forces solids are strained resulting in a change of volume and shape. In the approximation of the elastic continuum, the position of
each point of a solid is described by the vector 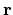 which in some Cartesian coordinate system has the components
which in some Cartesian coordinate system has the components 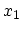 ,
, 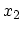 ,
, 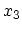 .
Under strain all points of a solid are in general shifted. If the position of a given point before strain was
.
Under strain all points of a solid are in general shifted. If the position of a given point before strain was 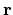 , then after strain it is
, then after strain it is
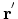 with components
with components 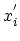 ,
, 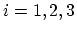 . The displacement of the point is characterized by the displacement vector defined as
. The displacement of the point is characterized by the displacement vector defined as
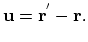 |
(3.9) |
The coordinates 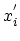 of a shifted point are functions of the coordinates
of a shifted point are functions of the coordinates 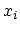 of the same point before strain. This means that the displacement
vector
of the same point before strain. This means that the displacement
vector 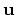 is also a function of
is also a function of 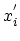 . This function completely determines the strained state of a solid.
. This function completely determines the strained state of a solid.
When a solid is strained, the distances between points change. If before strain the distance between two infinitely close points was 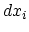 ,
then after strain it is equal to
,
then after strain it is equal to
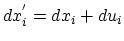 . The distance between these two points before strain is
. The distance between these two points before strain is
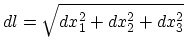 |
(3.10) |
and after strain:
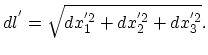 |
(3.11) |
Substituting the expressions for
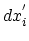 through
through 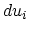 the following expression for
the following expression for 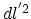 is obtained:
is obtained:
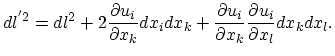 |
(3.12) |
Since indices in the double sum can be exchanged, the last expression can be rearranged and rewritten as:
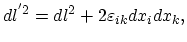 |
(3.13) |
where a tensor of the second rank has been introduced:
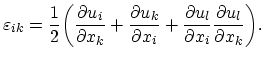 |
(3.14) |
The second rank tensor
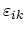 is called the strain tensor. As can be seen from the definition (3.14), it represents a symmetric
tensor:
is called the strain tensor. As can be seen from the definition (3.14), it represents a symmetric
tensor:
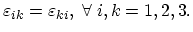 |
(3.15) |
Any symmetric tensor can be reduced to the principle axes. This means that at each given point the coordinate system can be chosen
in such a way that only diagonal elements
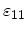 ,
,
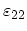 and
and
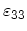 will be non-zero and all non-diagonal elements
vanish. It should be noted that if a tensor is reduced to the diagonal form at a given point, it will be in general non-diagonal at all other points of a
given solid considered as continuum.
will be non-zero and all non-diagonal elements
vanish. It should be noted that if a tensor is reduced to the diagonal form at a given point, it will be in general non-diagonal at all other points of a
given solid considered as continuum.
If the strain tensor is reduced at a given point to its principle axes, in the elementary volume built around this point the element of the length
(3.13) takes the form:
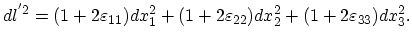 |
(3.16) |
This expression is decomposed into three independent terms. This means that at any given elementary volume of a solid the strain can
be considered as a set of three independent deformations along three relatively orthogonal directions - the principal axes of the tensor. Each of these
deformations represents a simple stretching or compressing along the corresponding direction: the length 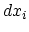 along the
along the 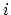 -th principle axis turns
into the length
-th principle axis turns
into the length
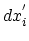 :
:
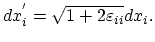 |
(3.17) |
The relative elongation along the 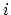 -th axis is thus given as:
-th axis is thus given as:
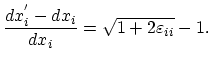 |
(3.18) |
A deformation is considered small if the change of any distance in a solid turns out to be much less than the distance
itself. In other words all relative elongations are much less than unity. In this work only strain of this kind is considered.
When strain is weak in the sense mentioned above, the displacements 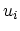 and their derivatives are small. Thus, in the general
expression (3.14) the last term is negligible and can be omitted. Therefore, in the case of weak strain, the components
and their derivatives are small. Thus, in the general
expression (3.14) the last term is negligible and can be omitted. Therefore, in the case of weak strain, the components
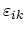 of the strain tensor are determined by the following expression:
of the strain tensor are determined by the following expression:
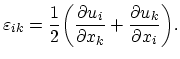 |
(3.19) |
In this case the relative elongations are thus equal:
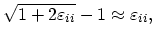 |
(3.20) |
and given by the eigen values of the strain tensor.
S. Smirnov:
![]() ,
then after strain it is equal to
,
then after strain it is equal to
![]() . The distance between these two points before strain is
. The distance between these two points before strain is
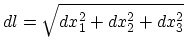
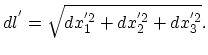
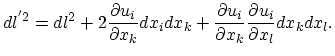
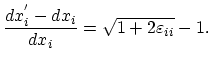
![]() and their derivatives are small. Thus, in the general
expression (3.14) the last term is negligible and can be omitted. Therefore, in the case of weak strain, the components
and their derivatives are small. Thus, in the general
expression (3.14) the last term is negligible and can be omitted. Therefore, in the case of weak strain, the components
![]() of the strain tensor are determined by the following expression:
of the strain tensor are determined by the following expression: