In the following a homogenous semiconductor is considered. Then the distribution function and the differential
scattering
rate are independent on position. It is also assumed that the differential scattering rate is time invariant. With these conditions the time dependent
Boltzmann
equation (2.60) taking into account the Pauli exclusion principle takes the following form:
,$](img825.png) |
(4.4) |
where
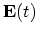 is an electric field and
is an electric field and 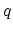 is the particle charge.
is the particle charge.
$](img827.png) represents the scattering operator which is given by the
following expression:
represents the scattering operator which is given by the
following expression:
where
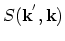 stands for the differential scattering rate. Thus
stands for the differential scattering rate. Thus
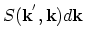 is the scattering rate from a state
with wave vector
is the scattering rate from a state
with wave vector
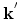 to states in
to states in 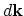 around
around 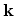 ,
,
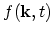 is the distribution function, and the factors
is the distribution function, and the factors
![$ [1-f(\vec{k},t)]$](img833.png) mean that the final state must not be occupied according to the Pauli exclusion principle. As can be seen from (4.6), there are terms
mean that the final state must not be occupied according to the Pauli exclusion principle. As can be seen from (4.6), there are terms
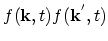 which render the equation nonlinear. Only when the condition
which render the equation nonlinear. Only when the condition
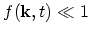 is valid the factors
is valid the factors
![$ [1-f(\vec{k},t)]$](img833.png) can be replaced by unity and the equation takes the usual linear form.
can be replaced by unity and the equation takes the usual linear form.
To linearize (4.4) the electric field is written in the form:
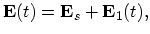 |
(4.6) |
where
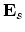 stands for a stationary field and
stands for a stationary field and
 denotes a small perturbation which is superimposed on a stationary field. It is
assumed that this small perturbation of the electric field causes a small perturbation of the distribution function which can be written as follows:
denotes a small perturbation which is superimposed on a stationary field. It is
assumed that this small perturbation of the electric field causes a small perturbation of the distribution function which can be written as follows:
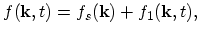 |
(4.7) |
where
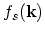 is a stationary distribution function and
is a stationary distribution function and
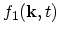 is a small deviation from a stationary distribution. Substituting
(4.8) into (4.6) the scattering operator
is a small deviation from a stationary distribution. Substituting
(4.8) into (4.6) the scattering operator
$](img827.png) takes the form:
takes the form:
It should be noted that in spite of the fact that
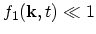 one should take care when linearizing terms such as
one should take care when linearizing terms such as
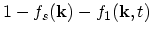 . Especially in the degenerate case it may happen that
. Especially in the degenerate case it may happen that
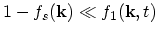 because of
because of
![$ [1-f_{s}(\vec{k})]\rightarrow 0$](img849.png) .
.
Subsections
S. Smirnov:
![$\displaystyle \int (f_{s}(\vec{k}^{'})+f_{1}(\vec{k}^{'},t))[1-f_{s}(\vec{k})-f_{1}(\vec{k},t)]S(\vec{k}^{'},\vec{k})\,d\vec{k}^{'}-$](img843.png)
![$\displaystyle \int (f_{s}(\vec{k})+f_{1}(\vec{k},t))[1-f_{s}(\vec{k}^{'})-f_{1}(\vec{k}^{'},t)]S(\vec{k},\vec{k}^{'})\,d\vec{k}^{'}.$](img845.png)