2.4 Topographiesimulation durch Lösung einer Diffusionsgleichung




Next: 2.4.1 Die Bewegung der
Up: 2 Analyse bestehender Algorithmen
Previous: 2.3.3 Dreidimensionale Simulation
Ein interessanter Ansatz für die Topographiesimulation wurde von Fujinaga
et al. [Fuj90] vorgestellt. Die Bewegung der Oberfläche wird
durch Lösen einer Diffusionsgleichung beschrieben, wobei sich
die Geometrie am Ende eines Zeitschrittes als Konturlinie der Lösungsfunktion
darstellt. Abbildung 2.31 zeigt einen Schnitt durch das
Simulationsgebiet.  stellt die Ätzmittelkonzentration und
stellt die Ätzmittelkonzentration und 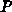 die
Materialkonzentration dar. Das Simulationsgebiet wird in drei Bereiche
unterteilt. Im Bereich I dominiert die Diffusion des Ätzmittels, die
chemischen Reaktion des Ätzmittels mit dem zu ätzenden Material wird
vernachlässigt. Im Bereich II kommt es gleichzeitig zu Diffusion des
Ätzmittels und chemischer Reaktion mit dem zu ätzenden Material, im
Bereich III sind beide Effekte vernachlässigbar. Die folgenden Gleichungen
beschreiben dieses Verhalten:
die
Materialkonzentration dar. Das Simulationsgebiet wird in drei Bereiche
unterteilt. Im Bereich I dominiert die Diffusion des Ätzmittels, die
chemischen Reaktion des Ätzmittels mit dem zu ätzenden Material wird
vernachlässigt. Im Bereich II kommt es gleichzeitig zu Diffusion des
Ätzmittels und chemischer Reaktion mit dem zu ätzenden Material, im
Bereich III sind beide Effekte vernachlässigbar. Die folgenden Gleichungen
beschreiben dieses Verhalten:
Bereich I:

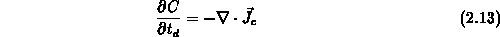
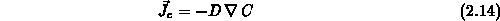
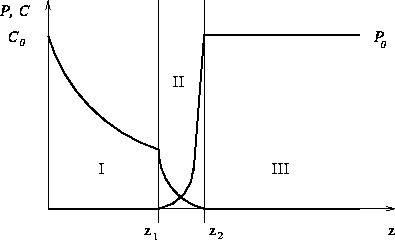
Abbildung 2.31: Material- und Ätzmittelkonzentration im Simulationsgebiet.
Bereich II:
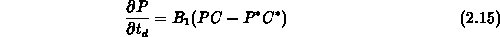
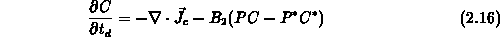
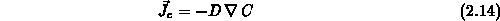
Bereich III:


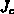 stellt den Diffussionsfluß des Ätzmittels und
stellt den Diffussionsfluß des Ätzmittels und 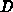 den zugehörigen
Diffusionskoeffizient dar.
den zugehörigen
Diffusionskoeffizient dar. 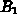 und
und 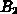 sind chemische Reaktionsraten,
sind chemische Reaktionsraten,
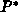 und
und 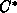 beschreiben die Material- und Ätzmittelkonzentration
im chemischen Gleichgewicht.
beschreiben die Material- und Ätzmittelkonzentration
im chemischen Gleichgewicht.
Im Bereich II dominiert im allgemeinen die chemische Reaktion gegenüber der
Diffusionsreaktion, sodaß gezeigt werden kann, daß die geometrische
Ausdehnung dieses Bereiches hinreichend klein gegenüber den Abmessungen der
Geometrie wird [Fuj90]. Unter dieser Vorraussetzung (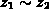 )
kann die Ätzfront nun durch den Ätzmittelkonzentrationswert an der Stelle
)
kann die Ätzfront nun durch den Ätzmittelkonzentrationswert an der Stelle
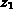 beschrieben werden. Der konstante Konzentrationswert
beginnt sich durch den Diffusionsprozeß weiter in das Material
hinein zu bewegen, es kommt damit zu einer Bewegung der Ätzfront.
beschrieben werden. Der konstante Konzentrationswert
beginnt sich durch den Diffusionsprozeß weiter in das Material
hinein zu bewegen, es kommt damit zu einer Bewegung der Ätzfront.
Unter der Annahme, daß der Diffusionskoeffizient nicht von der
Konzentration abhängt (lineares Diffusionsproblem), erhält man als
Lösung der Diffusionsgleichung im Bereich I [Cra75]
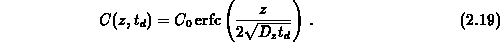
Die Lösungsfunktion beschreibt die Ätzmittelkonzentration für
das eindimensionale Problem unter der Annahme konstanter
Oberflächenkonzentration 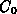 . Der geometrische Ort
. Der geometrische Ort  der
Ätzfront läßt sich damit als Funktion der Konzentration an der Stelle
der
Ätzfront läßt sich damit als Funktion der Konzentration an der Stelle
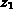 beschreiben
beschreiben
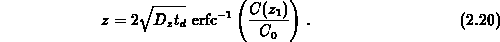
Damit erhält man für die Geschwindigkeit der Ätzfront
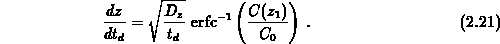
Aus Gleichung 2.22 und Gleichung 2.23 erkennt man, daß
die Distanz, um die sich die Ätzfront bewegt, proportional zu 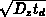 ist, wobei die Geschwindigkeit der Bewegung proportional zu
ist, wobei die Geschwindigkeit der Bewegung proportional zu 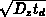 erfolgt. Setzt man für die Wurzel des Diffusionskoeffizienten
erfolgt. Setzt man für die Wurzel des Diffusionskoeffizienten
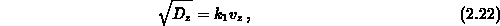
so wird aus Gleichung 2.22
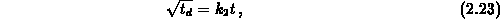
wobei 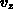 die Ätzrate des Materials beschreibt,
die Ätzrate des Materials beschreibt, 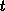 ist die zugehörige
Ätzzeit,
ist die zugehörige
Ätzzeit, 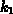 und
und 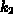 sind Proportionalitätskonstanten ohne weitere
physikalische Interpretation. Mit Gleichung 2.24 wird die Ätzzeit
sind Proportionalitätskonstanten ohne weitere
physikalische Interpretation. Mit Gleichung 2.24 wird die Ätzzeit
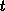 proportional zur Wurzel der Diffusionszeit
proportional zur Wurzel der Diffusionszeit 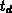 . Setzt man weiters
. Setzt man weiters
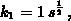
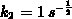 und
und 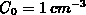 , so erhält man mit
, so erhält man mit 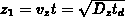 für den
Konzentrationswert an der Stelle
für den
Konzentrationswert an der Stelle 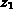 :
:
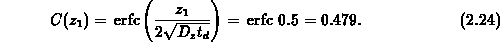
Das Prinzip der Methode besteht nun darin, diesen Konzentrationswert
während des Diffusionsprozesses zu verfolgen. Wählt man entsprechend
Gleichung 2.25 quadratische Diffussionszeitschritte,
also z.B. 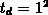 ,
,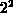 ,
, 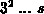 , so bewegt sich die Ätzfront
entsprechend der gewählten Ätzrate um lineare Wegstrecken. Die Ätzrate ist
dabei über Gleichung 2.24 mit dem Diffusionskoeffizienten
verknüpft.
, so bewegt sich die Ätzfront
entsprechend der gewählten Ätzrate um lineare Wegstrecken. Die Ätzrate ist
dabei über Gleichung 2.24 mit dem Diffusionskoeffizienten
verknüpft.
Abbildung 2.32 zeigt die Lösung des eindimensionalen
Diffusionsproblems in Abhängigkeit der Diffusionszeit,
Abbildung 2.33 zeigt die entsprechende Konturline für den
Konzentrationswert 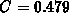 . Die Ätzrate für dieses Beispiel
beträgt
. Die Ätzrate für dieses Beispiel
beträgt 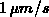 , der zugehörige Zeitschritt wurde zu
, der zugehörige Zeitschritt wurde zu 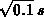 gewählt. Damit ergibt sich pro Zeitschritt ein zurückgelegter Weg
von 0.316
gewählt. Damit ergibt sich pro Zeitschritt ein zurückgelegter Weg
von 0.316 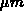 , wobei zu beachten ist, daß diese Wegstrecke
proportional zur Wurzel der Diffusionszeit anwächst (a = b).
, wobei zu beachten ist, daß diese Wegstrecke
proportional zur Wurzel der Diffusionszeit anwächst (a = b).
Die Bewegung der Ätzfront kann also durch die Lösung einer
Diffusionsgleichung beschrieben werden, wobei die Ätzrate und die Ätzzeit
über die Gleichung 2.24 und Gleichung 2.25 mit den
entsprechenden Größen des Diffusionsprozesses verknüpft sind. Für
die praktische Simulation wird die zwei- oder dreidimensionale Geometrie
durch quadratische oder würfelförmige Zellen beschrieben, wobei jeder
Zelle ein bestimmter Konzentrationswert zugeordnet wird.
Abbildung 2.34 zeigt das Prinzip des Algorithmus. Am Beginn
jedes Zeitschrittes besteht das Simulationsgebiet aus
Zellen, deren Konzentrationswert entweder 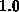 oder
oder 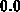 ist. Zellen mit
dem Konzentrationswert
ist. Zellen mit
dem Konzentrationswert 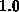 kennzeichnen Vakuumzellen während Zellen mit dem
Konzentrationswert
kennzeichnen Vakuumzellen während Zellen mit dem
Konzentrationswert 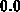 Materialzellen darstellen. Nach dem Lösen der
Diffusionsgleichung werden die Konzentrationswerte der Zellen
entsprechend dem Konzentrationswert
Materialzellen darstellen. Nach dem Lösen der
Diffusionsgleichung werden die Konzentrationswerte der Zellen
entsprechend dem Konzentrationswert 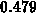 aus
Gleichung 2.26 umgesetzt. Zellen, deren Konzentrationswerte
unter dem Schwellwert liegen, bleiben Materialzellen alle übrigen
Zellen werden zu Vakuumzellen. Durch das Umsetzten der Konzentrationswerte
kommt es zu einer Bewegung der Oberfläche, die durch Materialzellen,
deren Nachbarzellen Vakuumzellen sind, beschrieben wird.
aus
Gleichung 2.26 umgesetzt. Zellen, deren Konzentrationswerte
unter dem Schwellwert liegen, bleiben Materialzellen alle übrigen
Zellen werden zu Vakuumzellen. Durch das Umsetzten der Konzentrationswerte
kommt es zu einer Bewegung der Oberfläche, die durch Materialzellen,
deren Nachbarzellen Vakuumzellen sind, beschrieben wird.




Next: 2.4.1 Die Bewegung der
Up: 2 Analyse bestehender Algorithmen
Previous: 2.3.3 Dreidimensionale Simulation
Martin Stiftinger
Thu Nov 24 17:41:25 MET 1994
 stellt die Ätzmittelkonzentration und
stellt die Ätzmittelkonzentration und 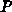 die
Materialkonzentration dar. Das Simulationsgebiet wird in drei Bereiche
unterteilt. Im Bereich I dominiert die Diffusion des Ätzmittels, die
chemischen Reaktion des Ätzmittels mit dem zu ätzenden Material wird
vernachlässigt. Im Bereich II kommt es gleichzeitig zu Diffusion des
Ätzmittels und chemischer Reaktion mit dem zu ätzenden Material, im
Bereich III sind beide Effekte vernachlässigbar. Die folgenden Gleichungen
beschreiben dieses Verhalten:
die
Materialkonzentration dar. Das Simulationsgebiet wird in drei Bereiche
unterteilt. Im Bereich I dominiert die Diffusion des Ätzmittels, die
chemischen Reaktion des Ätzmittels mit dem zu ätzenden Material wird
vernachlässigt. Im Bereich II kommt es gleichzeitig zu Diffusion des
Ätzmittels und chemischer Reaktion mit dem zu ätzenden Material, im
Bereich III sind beide Effekte vernachlässigbar. Die folgenden Gleichungen
beschreiben dieses Verhalten:





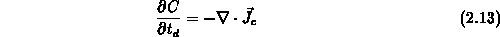
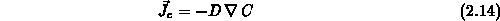

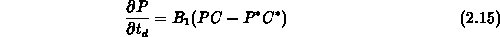
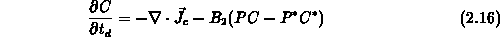


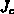 stellt den Diffussionsfluß des Ätzmittels und
stellt den Diffussionsfluß des Ätzmittels und 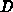 den zugehörigen
Diffusionskoeffizient dar.
den zugehörigen
Diffusionskoeffizient dar. 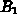 und
und 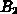 sind chemische Reaktionsraten,
sind chemische Reaktionsraten,
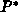 und
und 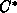 beschreiben die Material- und Ätzmittelkonzentration
im chemischen Gleichgewicht.
beschreiben die Material- und Ätzmittelkonzentration
im chemischen Gleichgewicht.
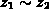 )
kann die Ätzfront nun durch den Ätzmittelkonzentrationswert an der Stelle
)
kann die Ätzfront nun durch den Ätzmittelkonzentrationswert an der Stelle
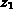 beschrieben werden. Der konstante Konzentrationswert
beginnt sich durch den Diffusionsprozeß weiter in das Material
hinein zu bewegen, es kommt damit zu einer Bewegung der Ätzfront.
beschrieben werden. Der konstante Konzentrationswert
beginnt sich durch den Diffusionsprozeß weiter in das Material
hinein zu bewegen, es kommt damit zu einer Bewegung der Ätzfront.
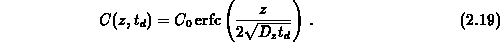
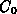 . Der geometrische Ort
. Der geometrische Ort  der
Ätzfront läßt sich damit als Funktion der Konzentration an der Stelle
der
Ätzfront läßt sich damit als Funktion der Konzentration an der Stelle
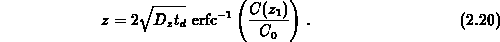
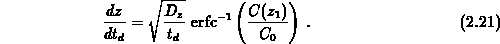
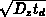 ist, wobei die Geschwindigkeit der Bewegung proportional zu
ist, wobei die Geschwindigkeit der Bewegung proportional zu 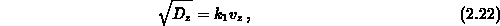
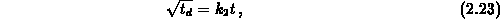
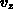 die Ätzrate des Materials beschreibt,
die Ätzrate des Materials beschreibt, 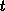 ist die zugehörige
Ätzzeit,
ist die zugehörige
Ätzzeit, 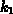 und
und 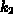 sind Proportionalitätskonstanten ohne weitere
physikalische Interpretation. Mit Gleichung
sind Proportionalitätskonstanten ohne weitere
physikalische Interpretation. Mit Gleichung 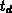 . Setzt man weiters
. Setzt man weiters
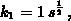
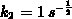 und
und 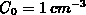 , so erhält man mit
, so erhält man mit 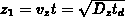 für den
Konzentrationswert an der Stelle
für den
Konzentrationswert an der Stelle 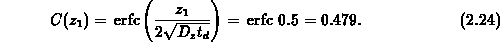
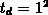 ,
,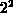 ,
, 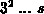 , so bewegt sich die Ätzfront
entsprechend der gewählten Ätzrate um lineare Wegstrecken. Die Ätzrate ist
dabei über Gleichung
, so bewegt sich die Ätzfront
entsprechend der gewählten Ätzrate um lineare Wegstrecken. Die Ätzrate ist
dabei über Gleichung 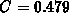 . Die Ätzrate für dieses Beispiel
beträgt
. Die Ätzrate für dieses Beispiel
beträgt 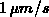 , der zugehörige Zeitschritt wurde zu
, der zugehörige Zeitschritt wurde zu 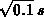 gewählt. Damit ergibt sich pro Zeitschritt ein zurückgelegter Weg
von 0.316
gewählt. Damit ergibt sich pro Zeitschritt ein zurückgelegter Weg
von 0.316 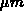 , wobei zu beachten ist, daß diese Wegstrecke
proportional zur Wurzel der Diffusionszeit anwächst (a = b).
, wobei zu beachten ist, daß diese Wegstrecke
proportional zur Wurzel der Diffusionszeit anwächst (a = b).
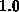 oder
oder 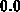 ist. Zellen mit
dem Konzentrationswert
ist. Zellen mit
dem Konzentrationswert 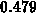 aus
Gleichung
aus
Gleichung