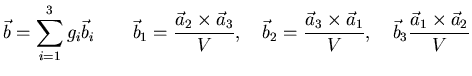


Next: 1.3 Bloch-Funktionen
Up: 1. Grundlagen
Previous: 1.1 Quantentheorie
Für die theoretische Behandlung der physikalischen Eigenschaften von
Halbleitern ist deren Kristallstruktur von entscheidender Bedeutung.
Im Halbleiter haben wir es mit einem Vielteilchenproblem zu tun, da
durch den Kristallverbund prinzipiell alle Teilchen miteinander in
Wechselwirkung stehen. Bereits bei der weitaus weniger dichten
Anordnung im idealen Gas hat man es pro Einheitsvolumen mit einer
Teilchenanzahl in der Größenordnung der Loschmid-Zahl zu tun. Diese
Datenmengen sind natürlich aus der Sicht der Datenverarbeitung nicht
unmittelbar beherrschbar. In der klassischen statistischen Mechanik
wird daher an Stelle einer Beschreibung des System durch die einzelnen
Mikrozustände nach Beziehungen zwischen makroskopischen Größen gesucht
([40]).
In der hier verwendeten quantenmechanischen Methode wollen wir
durch Ausnutzen von Symmetrieeigenschaften das System durch die
Beschreibung eines einzelnen charakteristischen Elektrons vornehmen.
Abbildung 1.1:
Kovalenter Bindungstyp mit vier Valenzelektronen in
planarer Projektion
![\includegraphics[]{Theorie/GeStrukt}](img103.png)
|
Silizium und andere Elementhalbleiter, wie Germanium, befinden sich
in der vierten Spalte (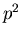 Elemente, Kohlenstoffgruppe) des
Periodensystems. Durch die Hybridisierung der vier Valenzelektronen
des ungestörten Siliziums beim Zusammenfügen in einer kristallinen
Struktur bilden sich vier kovalente Bindungen zu den nächsten
Nachbarn. Jede solche Bindung besteht aus je zwei Elektronen mit
entgegengesetztem Spin, entstanden aus einem
Elemente, Kohlenstoffgruppe) des
Periodensystems. Durch die Hybridisierung der vier Valenzelektronen
des ungestörten Siliziums beim Zusammenfügen in einer kristallinen
Struktur bilden sich vier kovalente Bindungen zu den nächsten
Nachbarn. Jede solche Bindung besteht aus je zwei Elektronen mit
entgegengesetztem Spin, entstanden aus einem  und einem
und einem 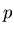 Zustand. Abbildung 1.1 soll diese Bindungen in
Form einer planaren Projektion am Beispiel des hinsichtlich der
Bindungen zu Silizium gleichwertigen Germanium skizzieren. Der dabei
entstehende Kristall liegt dann in der so genannten Diamantstruktur
beziehungsweise dem kubisch flächenzentrierten Gitter (siehe
Abbildung 1.2) vor.
Zustand. Abbildung 1.1 soll diese Bindungen in
Form einer planaren Projektion am Beispiel des hinsichtlich der
Bindungen zu Silizium gleichwertigen Germanium skizzieren. Der dabei
entstehende Kristall liegt dann in der so genannten Diamantstruktur
beziehungsweise dem kubisch flächenzentrierten Gitter (siehe
Abbildung 1.2) vor.
Abbildung 1.2:
Kubisch flächenzentriertes Gitter und Basisvektoren.
![\includegraphics[]{Theorie/FCCGitter}](img107.png)
|
Zur Beschreibung des idealen Kristallgitters wird grundsätzlich von
den Basisvektoren (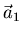 ,
, 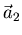 ,
, 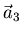 ), siehe
Abbildung 1.2 für den Fall des kubisch
flächenzentrierten Gitters) der sich periodisch im Raum wiederholenden
Elementarzelle ausgegangen. Die Gesamtheit aller durch beliebige
Verschiebung um eine Linearkombination dieser Basisvektoren
erreichbaren Punkte bildet das Bravais-Gitter.
Die Eigenschaften des Halbleiters werden somit durch die
Eigenschaften einer einzelnen Elementarzelle bestimmt.
), siehe
Abbildung 1.2 für den Fall des kubisch
flächenzentrierten Gitters) der sich periodisch im Raum wiederholenden
Elementarzelle ausgegangen. Die Gesamtheit aller durch beliebige
Verschiebung um eine Linearkombination dieser Basisvektoren
erreichbaren Punkte bildet das Bravais-Gitter.
Die Eigenschaften des Halbleiters werden somit durch die
Eigenschaften einer einzelnen Elementarzelle bestimmt.
Wir betrachten Funktionen 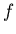 , welche die Periodizität
des Kristallgitters aufweisen.
, welche die Periodizität
des Kristallgitters aufweisen.
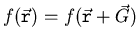 |
(1.4) |
Der Vektor 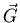 steht dabei für eine beliebige Linearkombination
der Basisvektoren des Kristallgitters.
Die Funktion
steht dabei für eine beliebige Linearkombination
der Basisvektoren des Kristallgitters.
Die Funktion 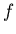 lässt sich durch eine Fourier-Reihe darstellen.
lässt sich durch eine Fourier-Reihe darstellen.
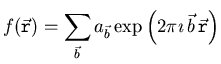 |
(1.5) |
Abbildung 1.3:
Brillouin-Zone des kubisch flächenzentrierten Gitters und
wichtige Symmetrieachsen und Symmetriepunkte.
![\includegraphics[]{Theorie/Brillouin}](img114.png)
|
Die Vektoren 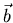 sollen dabei der Bedingung
sollen dabei der Bedingung
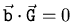 genügen. Dies wird durch die Vektoren des reziproken Gitters erfüllt.
genügen. Dies wird durch die Vektoren des reziproken Gitters erfüllt.
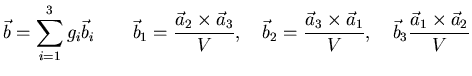 |
(1.6) |
Darin steht 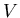 für das Volumen der Elementarzelle. Auch im reziproken
Gitter ist es sinnvoll eine Elementarzelle zu definieren. Eine
mögliche Definition ist dabei die Wigner-Seitz-Zelle, die auch als
Brillouin-Zone bekannt ist. Wie wir noch später erläutern werden, kann
man sich bei der Beschreibung des Kristalls im Fourier-Raum auf diese
Brillouin-Zone beschränken. Abbildung 1.3 zeigt
die Brillouin-Zone des kubisch flächenzentrierten Gitters und einige
wichtige Symmetrieachsen und Punkte.
für das Volumen der Elementarzelle. Auch im reziproken
Gitter ist es sinnvoll eine Elementarzelle zu definieren. Eine
mögliche Definition ist dabei die Wigner-Seitz-Zelle, die auch als
Brillouin-Zone bekannt ist. Wie wir noch später erläutern werden, kann
man sich bei der Beschreibung des Kristalls im Fourier-Raum auf diese
Brillouin-Zone beschränken. Abbildung 1.3 zeigt
die Brillouin-Zone des kubisch flächenzentrierten Gitters und einige
wichtige Symmetrieachsen und Punkte.



Next: 1.3 Bloch-Funktionen
Up: 1. Grundlagen
Previous: 1.1 Quantentheorie
C. Troger: Modellierung von Quantisierungseffekten in Feldeffekttransistoren
![\includegraphics[]{Theorie/GeStrukt}](img103.png)
![]() Elemente, Kohlenstoffgruppe) des
Periodensystems. Durch die Hybridisierung der vier Valenzelektronen
des ungestörten Siliziums beim Zusammenfügen in einer kristallinen
Struktur bilden sich vier kovalente Bindungen zu den nächsten
Nachbarn. Jede solche Bindung besteht aus je zwei Elektronen mit
entgegengesetztem Spin, entstanden aus einem
Elemente, Kohlenstoffgruppe) des
Periodensystems. Durch die Hybridisierung der vier Valenzelektronen
des ungestörten Siliziums beim Zusammenfügen in einer kristallinen
Struktur bilden sich vier kovalente Bindungen zu den nächsten
Nachbarn. Jede solche Bindung besteht aus je zwei Elektronen mit
entgegengesetztem Spin, entstanden aus einem ![]() und einem
und einem ![]() Zustand. Abbildung 1.1 soll diese Bindungen in
Form einer planaren Projektion am Beispiel des hinsichtlich der
Bindungen zu Silizium gleichwertigen Germanium skizzieren. Der dabei
entstehende Kristall liegt dann in der so genannten Diamantstruktur
beziehungsweise dem kubisch flächenzentrierten Gitter (siehe
Abbildung 1.2) vor.
Zustand. Abbildung 1.1 soll diese Bindungen in
Form einer planaren Projektion am Beispiel des hinsichtlich der
Bindungen zu Silizium gleichwertigen Germanium skizzieren. Der dabei
entstehende Kristall liegt dann in der so genannten Diamantstruktur
beziehungsweise dem kubisch flächenzentrierten Gitter (siehe
Abbildung 1.2) vor.
![]() ,
, ![]() ,
, ![]() ), siehe
Abbildung 1.2 für den Fall des kubisch
flächenzentrierten Gitters) der sich periodisch im Raum wiederholenden
Elementarzelle ausgegangen. Die Gesamtheit aller durch beliebige
Verschiebung um eine Linearkombination dieser Basisvektoren
erreichbaren Punkte bildet das Bravais-Gitter.
Die Eigenschaften des Halbleiters werden somit durch die
Eigenschaften einer einzelnen Elementarzelle bestimmt.
), siehe
Abbildung 1.2 für den Fall des kubisch
flächenzentrierten Gitters) der sich periodisch im Raum wiederholenden
Elementarzelle ausgegangen. Die Gesamtheit aller durch beliebige
Verschiebung um eine Linearkombination dieser Basisvektoren
erreichbaren Punkte bildet das Bravais-Gitter.
Die Eigenschaften des Halbleiters werden somit durch die
Eigenschaften einer einzelnen Elementarzelle bestimmt.
![]() , welche die Periodizität
des Kristallgitters aufweisen.
, welche die Periodizität
des Kristallgitters aufweisen.
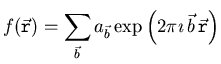
![\includegraphics[]{Theorie/Brillouin}](img114.png)