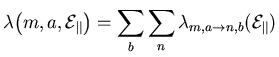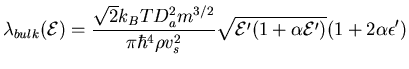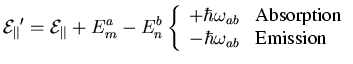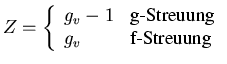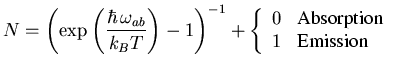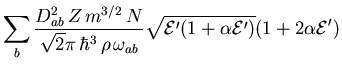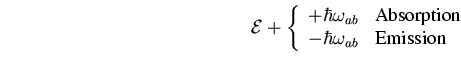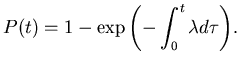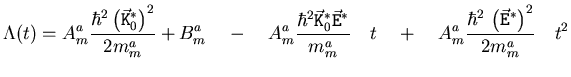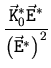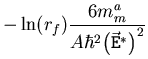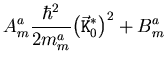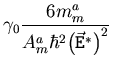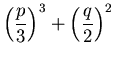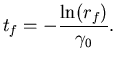


Next: 4.3 Statistische Auswertung
Up: 4. Transportberechnung
Previous: 4.1 Boltzmann-Gleichung
Unterabschnitte
Einen anderen Ansatz verfolgt man in der so genannten
Monte Carlo-Methode ([34]). Hier werden die Bewegungen der Ladungsträger unter der
Wirkung des angelegten Feldes und der auftretenden Streuungen durch
einen stochastischen Ansatz verfolgt. Die Methode ist deutlich
zeitaufwendiger als die Momentenmethode, bietet jedoch die Möglichkeit, Modelle für die
mikroskopischen Prozesse anzuwenden.
Aus diesem Grund ist die Monte Carlo-Methode bei der Behandlung des
Hochenergietransports und zur Bestimmung von Beweglichkeitsparametern
weit verbreitet.
Abbildung 4.1:
Flussdiagramm für ein Einteilchen-Monte Carlo-Programm.
|
|
Zwei Varianten sind bei diesem Ansatz für die Untersuchung des
Ladungsträgertransports grundsätzlich möglich. Zum einen kann eine
Vielzahl von Teichen gleichzeitig in Form einer Ensemble-Monte
Carlo-Simulation betrachtet werden. Zum anderen kann nur ein einzelnes
Teilchen über einen dementsprechend langen Zeitraum betrachtet
werden. Aus dem Ergodentheorem folgt die ─quivalenz von
Scharmittelwert und Zeitmittelwert. In diesem Sinne führen beide
Varianten im stationären Fall zum gleichen Resultat. Im Folgenden
wollen wir nun die zweite Variante anwenden.
Die Bahn des Ladungsträgers wird semiklassisch verfolgt. Zwei
Vorgänge sind für den Transport des Ladungsträgers von Bedeutung. Zum
einen verhält sich das Elektron im treibenden elektrischen Feld wie
ein freies Teilchen und wird in der Ebene normal zur
Quantisierungsrichtung von diesem beschleunigt. Bei der Ableitung der
Bewegungsgleichung wird für die Energie die Dispersionsrelation des
gerade aktuellen Subbandes herangezogen. Zum anderen erfolgt nach
einer noch zu definierenden freien Flugzeit eine Wechselwirkung mit
den Störungen des Kristallgitters in Form einer Streuung. Nur durch
eine solche Streuung kann das Elektron in einen durch ein anderes
Subband oder eine andere Talsorte charakterisierten Zustand gelangen.
Sowohl die Auswahl der Dauer des freien Flugs als auch die Auswahl des
Streuprozesses erfolgen über Zufallszahlen. Der prinzipielle Ablauf
einer Einteilchen-Monte Carlo-Simulation ist in
Abbildung 4.1 dargestellt.
Die Energie in Parallelrichtung hängt von der so genannten
Bandformfunktion ab.
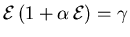 |
(4.3) |
Für die X-Täler in Silizium sind die effektiven
Massen zu berücksichtigen.
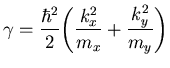 |
(4.4) |
Um diese Anisotropie in den Formeln zu eliminieren empfiehlt sich
eine Transformation nach Herring und Vogt ([18]).
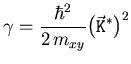 |
(4.5) |
Als Abkürzung wurde hier der transformierte Wellenvektor mit einem
eigenen Symbol
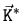 versehen.
versehen.
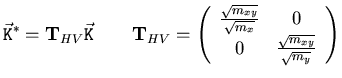 |
(4.6) |
Bei den in Kapitel 2.2.1 eingeführten Talsorten wird nun
mit der Transformation (4.6), entsprechend den drei Achsen,
mit drei verschiedenen Talsorten gerechnet.
Abbildung 4.2:
Aufstellung der effektiven Massen in den einzelnen Talsorten.
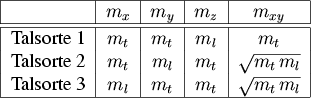 |
In Tabelle 4.2 sind die in den verschiedenen
Talsorten verwendeten Massen angegeben.
Die zeitliche Entwicklung des transformierten Wellenvektors erhält
man aus den Newton'schen Bewegungsgleichungen. Es soll in der Parallelebene
ein konstantes Feld
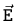 herrschen. Für den Impuls des Teilchens
gilt das Newton'sche Gesetz.
herrschen. Für den Impuls des Teilchens
gilt das Newton'sche Gesetz.
 |
(4.7) |
Multipliziert man diese Gleichung von links mit
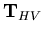 , ergibt sich
, ergibt sich
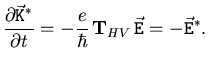 |
(4.8) |
Für ein konstantes Feld erhält man aus Gleichung (4.8)
eine einfache Zeitentwicklung des Wellenvektors .
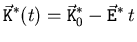 |
(4.9) |
Für die Bewegungsgleichung im Ortsraum geht man von der
Gruppengeschwindigkeit
aus. Der Nenner in (4.10) kann als
Leitfähigkeits-Effektive-Masse 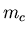 definiert werden.
definiert werden.
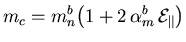 |
(4.11) |
Diese Masse ist über die Energie auch von der Zeit abhängig. Im
Simulator soll jedoch für jeden einzelnen freien Flug die Energie in
dieser Formel als konstant angesehen werden. Einmaliges Integrieren
der Gleichung (4.10) ergibt dann die zeitliche Entwicklung
des Ortsvektors.
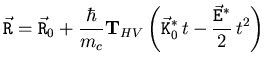 |
(4.12) |
Abbildung 4.3:
Skizze einer Streuung zwischen zwei Subbändern in
verschiedenen Tälern.
|
|
Die Wechselwirkung des Elektrons mit den Gitterstörungen wird durch
Streuungen berücksichtigt. Bei den Gitterschwingungen
wird die Zeitabhängigkeit des Streupotenzial durch einen
Ansatz mit der Kreisfrequenz 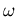 dargestellt.
dargestellt.
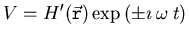 |
(4.13) |
Die ▄bergangswahrscheinlichkeit vom Zustand mit dem
Wellenvektor
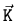 im Subband
im Subband 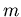 und Tal
und Tal 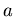 in den durch Wellenvektor
in den durch Wellenvektor
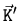 , Subband
, Subband 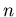 und Tal
und Tal 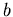 charakterisierten Zustand ergibt sich nach der
Goldenen Regel der Quantenmechanik
([38, Kap. 16.3], [45]).
charakterisierten Zustand ergibt sich nach der
Goldenen Regel der Quantenmechanik
([38, Kap. 16.3], [45]).
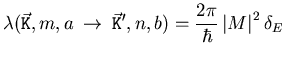 |
(4.14) |
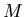 steht dabei für das Matrixelement des Störungsoperators
und die Deltafunktion für die Erhaltung der Energie. Durch
die Wechselwirkung kommt es zum Austausch eines Energiequants
steht dabei für das Matrixelement des Störungsoperators
und die Deltafunktion für die Erhaltung der Energie. Durch
die Wechselwirkung kommt es zum Austausch eines Energiequants
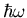 mit dem Gitter.
mit dem Gitter.
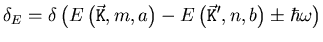 |
(4.15) |
Setzt man das Streupotenzial aus Gleichung (4.13) in das
Matrixelement ein so erhält man
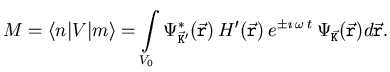 |
(4.16) |
Die vorkommende Zeitabhängigkeit ändert nur die Phase und fällt bei
der Bildung der benötigten Betragsquadrate des Matrixelements
weg. Der verbleibende Term wird nun in der Fourier-Darstellung
behandelt.
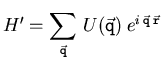 |
(4.17) |
Im Falle des zweidimensionalen Elektronengases werden die Elektronen
durch eine ebene Welle in Parallelrichtung und eine einhüllenden
Funktionen in Quantisierungsrichtung dargestellt. Setzt man diesen
Ansatz in die Berechnung der Matrixelemente ein, so ergibt sich:
Die Deltafunktion in (4.18) verknüpft die mögliche Veränderung des
Wellenvektors
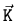 und die in der Fourier-Darstellung
vorkommenden Wellenvektoren
und die in der Fourier-Darstellung
vorkommenden Wellenvektoren
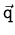 .
Weiters müssen die so genannten ▄berlappungsintegrale
.
Weiters müssen die so genannten ▄berlappungsintegrale
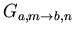 berechnet werden.
Sie ergeben sich durch Integration über die mit der Funktion
berechnet werden.
Sie ergeben sich durch Integration über die mit der Funktion
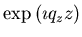 gewichteten einhüllenden Funktionen,
die aus der Lösung der Schrödinger-Gleichung erhalten wurden.
gewichteten einhüllenden Funktionen,
die aus der Lösung der Schrödinger-Gleichung erhalten wurden.
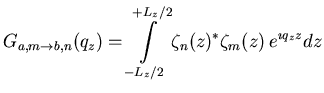 |
(4.19) |
Mit den bisher erhaltenen Ergebnissen stellt sich die Streurate nun
wie folgt dar.
Die Parallelkomponente von
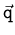 ist auf die Differenz der
Parallelkomponente des Wellenvektor vor und nach der Streuung
eingeschränkt. Die Summation über die verbleibende Komponente
ist auf die Differenz der
Parallelkomponente des Wellenvektor vor und nach der Streuung
eingeschränkt. Die Summation über die verbleibende Komponente
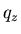 wurde in eine Integration umgewandelt.
Für Streupotenziale die nicht explizit von dieser Komponente abhängen
kann man eine weitere Vereinfachung vornehmen. Die
▄berlappungsintegrale erhalten die Bedeutung von effektiven Weiten.
wurde in eine Integration umgewandelt.
Für Streupotenziale die nicht explizit von dieser Komponente abhängen
kann man eine weitere Vereinfachung vornehmen. Die
▄berlappungsintegrale erhalten die Bedeutung von effektiven Weiten.
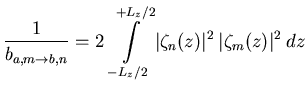 |
(4.21) |
In der Streurate kommt dann nur noch der Term aus dem Ansatz des
Streupotenzials, die effektive Weite und die für die Energieerhaltung
verantwortliche Deltafunktion vor.
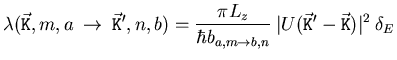 |
(4.22) |
Die Streurate für den ▄bergang von einem Ausgangszustand im
Subband 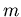 im Tal
im Tal 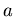 in ein Subband
in ein Subband 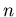 im Tal
im Tal 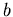 ergibt sich durch
Integrieren über alle erlaubten
Parallelkomponenten des Wellenvektors im Endzustand.
ergibt sich durch
Integrieren über alle erlaubten
Parallelkomponenten des Wellenvektors im Endzustand.
Unter Verwendung der effektive Weiten kann die Integration über
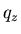 ausgeführt werden.
ausgeführt werden.
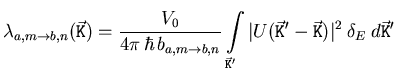 |
(4.24) |
Darin bedeuten 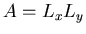 und
und
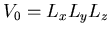 das betrachtete Volumen.
Um die gesamte Streurate für einen Zustand im Tal
das betrachtete Volumen.
Um die gesamte Streurate für einen Zustand im Tal 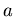 und Subband
und Subband 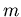 zu erhalten, ist noch die Summe über alle Subbänder
zu erhalten, ist noch die Summe über alle Subbänder 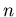 in allen
möglichen Endtälern
in allen
möglichen Endtälern 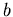 zu berechnen.
zu berechnen.
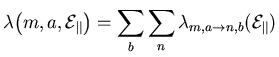 |
(4.25) |
Für die akustischen Phononen kann man die Dispersionsrelation der
Phononen für die hier betrachteten kleinen Werte der Wellenzahl
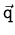 durch eine Gerade mit der Steigung
durch eine Gerade mit der Steigung
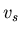 annähern. Dabei ist
annähern. Dabei ist
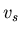 die Schallgeschwindigkeit im Kristall. Der Streuprozess
führt nicht in eine andere Talsorte und wird des weiteren in der
,,─quipartitions-Näherung``([18]) als elastisch
betrachtet. Deshalb muss im Gegensatz zu den inelastischen
Phononen-Streuprozessen nicht zwischen Emission und Absorption
unterschieden werden.
die Schallgeschwindigkeit im Kristall. Der Streuprozess
führt nicht in eine andere Talsorte und wird des weiteren in der
,,─quipartitions-Näherung``([18]) als elastisch
betrachtet. Deshalb muss im Gegensatz zu den inelastischen
Phononen-Streuprozessen nicht zwischen Emission und Absorption
unterschieden werden.
In (4.26) steht 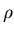 für die Dichte des
Kristalls,
für die Dichte des
Kristalls, 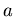 für die Talsorte und
für die Talsorte und 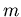 für den Subbandindex des
Ausgangszustands,
für den Subbandindex des
Ausgangszustands, 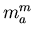 für die effektive Masse im
Subband
für die effektive Masse im
Subband 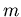 der Talsorte
der Talsorte 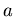 ,
, 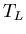 für die Gittertemperatur und
für die Gittertemperatur und 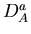 für das Deformationspotenzial. Die Energie des
Endzustands,bezogen auf das Energieminimum des Endsubbands, ergibt
sich aus der Differenz der Subbandenergien.
für das Deformationspotenzial. Die Energie des
Endzustands,bezogen auf das Energieminimum des Endsubbands, ergibt
sich aus der Differenz der Subbandenergien.
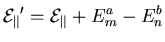 |
(4.27) |
Als Vergleich sei noch die Streurate für den nicht quantisierten Fall
angegeben.
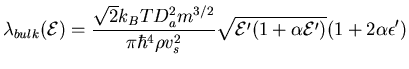 |
(4.28) |
Hier bleibt die Energie des Elektrons unverändert,
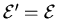 .
.
Abbildung 4.4:
Streuraten zur akustischen Deformationspotenzialstreuung.
|
|
In Abbildung 4.4 sind die nichtquantisierte
akustische Deformationspotenzialstreuung und die quantisierten
Streuraten für zwei unterschiedliche Talsorten aufgetragen. Für den
Transport in Parallelrichtung ist nach
Tabelle 2.2 wegen der verwendeten
Herring-Vogt-Transformation in zwei von drei Talsorten die gleiche
effektive Bewegungsmasse
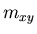 zu verwenden.
zu verwenden.
Bei diesen Streumechanismen kann die Dispersionsrelation der Phononen
durch eine Konstante angenähert werden. Der Zustand nach der Streuung
kann in derselben (g-Streuung) oder einer anderen Talsorte
(f-Streuung) als jener des Ausgangszustandes liegen. Des weiteren sind
nach [18, Appendix C] vier Streuungen zu berücksichtigen.
Es handelt sich nun
um einen inelastischen Streuprozess. Bei der Absorption eines Phonons
wird ein Energiequant
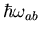 aufgenommen, im
Falle einer Emission dieser Energiebetrag abgegeben.
aufgenommen, im
Falle einer Emission dieser Energiebetrag abgegeben.
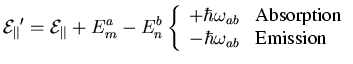 |
(4.30) |
Für die Entartung
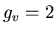 der vorliegenden Talsorten muss
zwischen dem ▄bergang in die gleiche oder eine andere Talsorte
unterschieden werden. Streut das Elektron in die gleiche Talsorte,
stehen nur
der vorliegenden Talsorten muss
zwischen dem ▄bergang in die gleiche oder eine andere Talsorte
unterschieden werden. Streut das Elektron in die gleiche Talsorte,
stehen nur
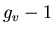 mögliche Endtäler zur Verfügung. Dies wurde
in der Streurate (4.29) durch den Parameter
mögliche Endtäler zur Verfügung. Dies wurde
in der Streurate (4.29) durch den Parameter 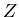 berücksichtigt.
berücksichtigt.
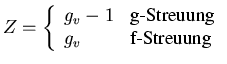 |
(4.31) |
Der Parameter 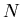 ergibt sich aus der Bose-Einstein-Statistik.
ergibt sich aus der Bose-Einstein-Statistik.
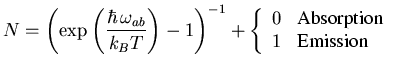 |
(4.32) |
Zum Vergleich sei wieder die nicht quantisierte Streurate angegeben.
Abbildung 4.5:
Zwischentalstreuung für ein Elektron im ersten Subband.
|
|
Abbildung 4.6:
Zwischentalstreuung in verschiedenen Ausgangssubbändern.
|
|
In Abbildung 4.5 ist die nichtquantisierte
Zwischentalstreuung und die quantisierten
Streurate für den ▄bergang zwischen verschiedenen Talsorten
aufgetragen. Bei den quantisierten Streuraten wurde
zwischen Ausgangstal und Endtal unterschieden.
Den grö▀ten Beitrag zur Gesamtstreurate liefert die Streuung
zwischen zwei Tälern der gleichen Sorte.
Bei den quantisierten Streuraten wird die Energie
jeweils vom Eigenwert des Ausgangssubbands im Ausgangstal gemessen.
Die Streuraten aus den energetisch höher gelegenen Subbändern
sind höher als jene aus den tiefer gelegenen Subbändern.
Dies ist in Abbildung 4.6 zu erkennen. Bei den
hier gezeigten Streuraten wurde das erste, zweite und dritte
Subband der Talsorte 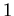 als Ausgangssubband verwendet.
als Ausgangssubband verwendet.
4.2.4 Freie Flugzeit
Es sei
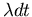 die Wahrscheinlichkeit mit der ein Teilchen
im Zeitintervall
die Wahrscheinlichkeit mit der ein Teilchen
im Zeitintervall
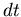 gestreut wird. Zum Zeitpunkt
gestreut wird. Zum Zeitpunkt
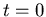 soll ein Streuereignis
stattgefunden haben. Zum Zeitpunkt
soll ein Streuereignis
stattgefunden haben. Zum Zeitpunkt
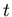 lautet dann die
Wahrscheinlichkeit dafür, dass noch keine neue Streuung stattgefunden
hat ([18])
lautet dann die
Wahrscheinlichkeit dafür, dass noch keine neue Streuung stattgefunden
hat ([18])
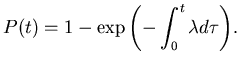 |
(4.34) |
Aus dieser Wahrscheinlichkeitsverteilung wird nun über eine
Folge von gleichverteilten Zufallszahlen
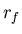 eine Folge
von freien Flugzeiten
eine Folge
von freien Flugzeiten
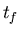 aus
aus
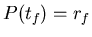 ermittelt.
ermittelt.
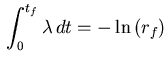 |
(4.35) |
Die Berechnung des Integrals über die Streuraten ist jedoch aufgrund
der Komplexität der Streuraten aufwendig und kann durch Einführen
eines Selbststreuprozesses vereinfacht werden.
Dieser spezielle Streuprozess ändert den Zustand des Ladungsträgers
nicht. Er dient nur dazu, den Verlauf der gesamten Streurate in eine
einfache analytische Funktion zu transformieren, aus der die freie Flugzeit
leichter berechnet werden kann. Dazu benötigt man
eine obere Abschätzung für die gesamte Streurate wie sie in
Abbildung 4.7 skizziert ist. Von den
verschieden Ansätzen [18] wird hier die in [24, Kapitel
5] beschriebene Methode verwendet. Dabei wird eine lineare
Begrenzungsfunktion zu den Streuraten bestimmt und über diese der
Selbststreuprozess definiert. Dieser Selbststreuprozess
verändert zwar den Zustand des Elektrons
nicht, wird aber als zusätzlicher Streuprozess in der Monte Carlo-Methode berücksichtigt.
Abbildung 4.7:
Skizze zur Definition des Selbststreuprozesses.
|
|
Die Begrenzungsfunktion
der Streurate in der Form
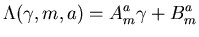 |
(4.36) |
ist pro Subband und Talsorte aus den Streuraten zu ermitteln.
Die Koeffizienten 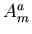 werden über einen least-square
Algorithmus berechnet.
Als Stützstellen werden dabei all jene Energiewerte verwendet,
bei denen die Streurate aufgrund eines möglichen Wechsels
in ein anderes Subband einen Sprung aufweist.
Um den Koeffizienten
werden über einen least-square
Algorithmus berechnet.
Als Stützstellen werden dabei all jene Energiewerte verwendet,
bei denen die Streurate aufgrund eines möglichen Wechsels
in ein anderes Subband einen Sprung aufweist.
Um den Koeffizienten 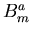 zu erhalten,
wird die Gerade mit der Steigung
zu erhalten,
wird die Gerade mit der Steigung 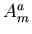 solange verschoben, bis die
Werte der Streuraten an den Stützstellen unter ihr zu liegen kommen.
Somit ist sichergestellt, dass die Streurate immer kleiner ist als
die Begrenzungsfunktion.
solange verschoben, bis die
Werte der Streuraten an den Stützstellen unter ihr zu liegen kommen.
Somit ist sichergestellt, dass die Streurate immer kleiner ist als
die Begrenzungsfunktion.
Den zeitlichen Verlauf der Begrenzungsfunktion kann man nun durch
Einsetzen der Bandformfunktion und der
Zeitentwicklung (4.9) des
Wellenvektors ermitteln.
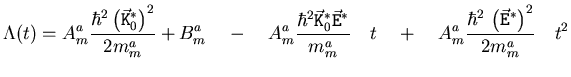 |
(4.37) |
Setzt man diese Funktion in (4.35) zur
Bestimmung der freien Flugzeit
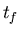 ein so ergibt sich
eine kubische Gleichung mit folgenden Koeffizienten.
ein so ergibt sich
eine kubische Gleichung mit folgenden Koeffizienten.
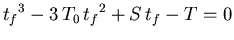 |
(4.38) |
Mit diesen Koeffizienten folgt für die freie Flugzeit bei einer
positiven Diskriminante D die reelle Lösung aus der Formel von
Cardano ([8, Abschnitt 4.5]):
![$\displaystyle {} t_f = T_0 + \sqrt[3]{-\frac{q}{2}+\sqrt{D}} + \sqrt[3]{-\frac{q}{2}-\sqrt{D}}$](img629.png) |
(4.39) |
Für die Anwendbarkeit der Formel (4.39)
müssen die Voraussetzungen 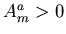 und
und 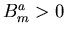 erfüllt sein, damit
erfüllt sein, damit 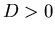 gilt.
gilt.
Im feldfreien Fall sind die angegebenen Koeffizienten nicht
definiert. Es ergibt sich für die Lösung die
einfachere Formel
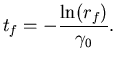 |
(4.40) |



Next: 4.3 Statistische Auswertung
Up: 4. Transportberechnung
Previous: 4.1 Boltzmann-Gleichung
C. Troger: Modellierung von Quantisierungseffekten in Feldeffekttransistoren
![\includegraphics[]{MC/MCablauf-fin.eps}](img531.png)
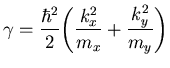
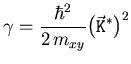
![]() herrschen. Für den Impuls des Teilchens
gilt das Newton'sche Gesetz.
herrschen. Für den Impuls des Teilchens
gilt das Newton'sche Gesetz.
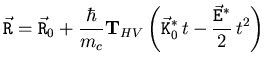
![]() im Subband
im Subband ![]() und Tal
und Tal ![]() in den durch Wellenvektor
in den durch Wellenvektor
![]() , Subband
, Subband ![]() und Tal
und Tal ![]() charakterisierten Zustand ergibt sich nach der
Goldenen Regel der Quantenmechanik
([38, Kap. 16.3], [45]).
charakterisierten Zustand ergibt sich nach der
Goldenen Regel der Quantenmechanik
([38, Kap. 16.3], [45]).
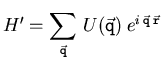
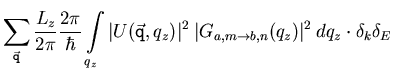
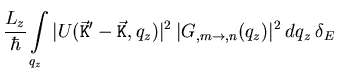
![]() im Tal
im Tal ![]() in ein Subband
in ein Subband ![]() im Tal
im Tal ![]() ergibt sich durch
Integrieren über alle erlaubten
Parallelkomponenten des Wellenvektors im Endzustand.
ergibt sich durch
Integrieren über alle erlaubten
Parallelkomponenten des Wellenvektors im Endzustand.