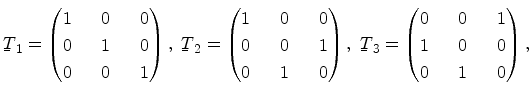3.5.5 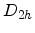 symmetry
symmetry
Figure 3.10:
Irreducible wedge of the first BZ of a diamond structure stressed along direction [110].
|
|
The Bravais cube of the crystal class 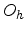 can be converted to a
parallelepiped of the orthorhombic system belonging to
can be converted to a
parallelepiped of the orthorhombic system belonging to 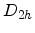 in two
ways [Bir74]:
in two
ways [Bir74]:
- Dilatation or compression along two of the three fourfold axes
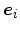 . This results in a right parallelepiped with rectangular faces
(cuboid). Of the five twofold axes
. This results in a right parallelepiped with rectangular faces
(cuboid). Of the five twofold axes
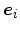 and
and
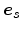 of
of 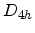 , only the three
, only the three
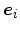 along the edges of the parallelepiped remain. This symmetry reduction can be
achieved by applying stress of different magnitude along two of the three
equivalent
along the edges of the parallelepiped remain. This symmetry reduction can be
achieved by applying stress of different magnitude along two of the three
equivalent
 directions, simultaneously. In this case, the
strain tensor is given by
directions, simultaneously. In this case, the
strain tensor is given by
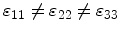 and contains
vanishing off-diagonal components.
and contains
vanishing off-diagonal components.
- The deformation originates from shearing the unit cube, thus altering
the angles between the basis vectors. The result is a rectangular
parallelepiped with rhombic base, which is also invariant under
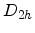 . Of
the original five twofold axes
. Of
the original five twofold axes
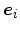 and
and
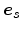 only two
(diagonals of the base) remain. This type of lattice results,
when uniaxial stress is applied along
only two
(diagonals of the base) remain. This type of lattice results,
when uniaxial stress is applied along
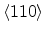 or from biaxial
strain in a {110} plane. The strain tensor has the form
or from biaxial
strain in a {110} plane. The strain tensor has the form
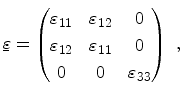 |
(3.44) |
where the components of the strain tensor can be related to stress according to
(3.18).
This group has only eight symmetry elements (given in
Table 3.2). The irreducible wedge with a volume of
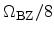 can be mapped onto six wedges of the unstrained
lattice in the limit of vanishing strain.
can be mapped onto six wedges of the unstrained
lattice in the limit of vanishing strain.
When dilating or compressing along two of the three fourfold axes
 (case 1), any octant of the BZ can be chosen as the irreducible wedge. In the
presence of uniaxial stress along [110] (case 2) a possible choice for the
irreducible wedge is depicted in Figure 3.10. The six wedges labeled
in Figure 3.10 can be transformed into the first wedge by the
transformations
(case 1), any octant of the BZ can be chosen as the irreducible wedge. In the
presence of uniaxial stress along [110] (case 2) a possible choice for the
irreducible wedge is depicted in Figure 3.10. The six wedges labeled
in Figure 3.10 can be transformed into the first wedge by the
transformations
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology
![\includegraphics[scale=1.0, clip]{inkscape/bz110_colored.eps}](img381.png)
![]() can be converted to a
parallelepiped of the orthorhombic system belonging to
can be converted to a
parallelepiped of the orthorhombic system belonging to ![]() in two
ways [Bir74]:
in two
ways [Bir74]:
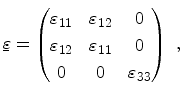
![]() can be mapped onto six wedges of the unstrained
lattice in the limit of vanishing strain.
can be mapped onto six wedges of the unstrained
lattice in the limit of vanishing strain.
![]() (case 1), any octant of the BZ can be chosen as the irreducible wedge. In the
presence of uniaxial stress along [110] (case 2) a possible choice for the
irreducible wedge is depicted in Figure 3.10. The six wedges labeled
in Figure 3.10 can be transformed into the first wedge by the
transformations
(case 1), any octant of the BZ can be chosen as the irreducible wedge. In the
presence of uniaxial stress along [110] (case 2) a possible choice for the
irreducible wedge is depicted in Figure 3.10. The six wedges labeled
in Figure 3.10 can be transformed into the first wedge by the
transformations