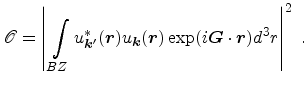The collision integral at the right hand side of Boltzmann's transport
equation is defined as the rate of change of the distribution function
It describes the transition from an arbitrary state
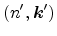 into the
state
into the
state
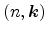 and the reverse process assuming that scattering does not
change the particle's spin. The probability density rate for a transition from
the initial state
and the reverse process assuming that scattering does not
change the particle's spin. The probability density rate for a transition from
the initial state
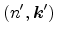 to a final state
to a final state
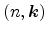 depends on
position and is proportional to the occupancy of the initial state
depends on
position and is proportional to the occupancy of the initial state
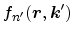 , proportional to the transition rate
, proportional to the transition rate
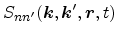 , and to the probability that the final
state is not occupied
, and to the probability that the final
state is not occupied
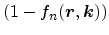 . The latter factor is a
result of the Pauli Principle and will be discussed in more detail in
Section 5.4.
. The latter factor is a
result of the Pauli Principle and will be discussed in more detail in
Section 5.4.
Omitting time and position dependence for the sake of brevity, the scattering rates are defined as
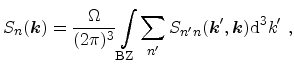 |
(5.8) |
where the integration can be performed over the first BZ or any primitive cell
in the reciprocal space. The scattering rate represents the rate at which
particles are scattered out of the initial state
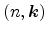 . From Fermi's
Golden Rule it follows that the scattering rates are proportional to the final
density of states per spin,
. From Fermi's
Golden Rule it follows that the scattering rates are proportional to the final
density of states per spin,
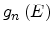 , which is given by
, which is given by
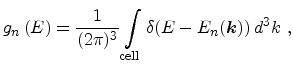 |
(5.9) |
In fullband MC simulations this integral is evaluated numerically. Using
an analytical description for the conduction bands, the minima of the
conduction bands (valleys) are approximated using the bandform function
Note that the band index  was replaced by the valley index
was replaced by the valley index 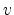 , and
, and 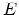 denotes the energy with respect to the valley offset
denotes the energy with respect to the valley offset 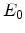 .
.
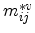 denotes the effective mass tensor, and
denotes the effective mass tensor, and
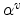 the nonparabolicity
coefficient of the valley with index
the nonparabolicity
coefficient of the valley with index 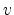 . A parabolic band dispersion is
obtained if the nonparabolicity coefficient
. A parabolic band dispersion is
obtained if the nonparabolicity coefficient 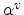 is zero.
is zero.
The density of states of the analytical band structure evaluates to
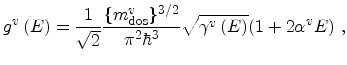 |
(5.12) |
where
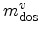 denotes the density of states mass of the
denotes the density of states mass of the 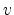 -th valley
-th valley
![$\displaystyle m^v_\mathrm{dos}= \sqrt[3]{ \{m^*_{11}\}^v \{m^*_{22}\}^v \{m^*_{33}\}^v } \ ,%\vphantom{\sum_i}
$](img872.png) |
(5.13) |
which can be calculated from the effective mass tensor.
The transition rates from state
(
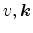 ) to state (
) to state (
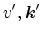 ) for phonon
scattering in a non-polar semiconductor can be written as [Jacoboni83]
) for phonon
scattering in a non-polar semiconductor can be written as [Jacoboni83]
![$\displaystyle \{\tiny S^{ \shortstack{abs \\ [-2pt] emi }} \} ^{v'v}({\ensurema...
...ath{\mathitbf{k}}}') - E^{v}({\ensuremath{\mathitbf{k}}}) \mp \hbar\omega_q]\ .$](img875.png) |
(5.14) |
Here, the upper and lower symbols refer to phonon absorption and emission,
respectively. The rate depends on the momentum transfer
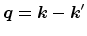 , the phonon number
, the phonon number 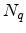 , the deformation potential tensor
, the deformation potential tensor
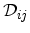 , the mass density of the crystall
, the mass density of the crystall 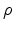 , the phonon angular frequency
, the phonon angular frequency
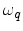 , its polarization
, its polarization 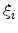 , and the overlap
integral
, and the overlap
integral
 ,
,
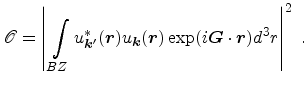 |
(5.15) |
The overlap factors depend on the type of transition. For intravalley
transitions of electrons,
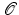 is frequently set to unity, even though
this is true only for exact plane waves or for wave functions formed with pure
is frequently set to unity, even though
this is true only for exact plane waves or for wave functions formed with pure
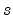 states [Jacoboni83]. Because the lowest conduction band of cubic
semiconductors is a mixture of a
states [Jacoboni83]. Because the lowest conduction band of cubic
semiconductors is a mixture of a 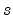 and
and 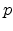 -type state, an overlap factor less
than unity is obtained.
Both for intra- and intervalley transitions
-type state, an overlap factor less
than unity is obtained.
Both for intra- and intervalley transitions
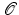 was found to be almost constant for each type of scattering
process [Reggiani73], thus the values for
was found to be almost constant for each type of scattering
process [Reggiani73], thus the values for
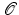 may be included in
the coupling constants.
may be included in
the coupling constants.
Subsections
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology
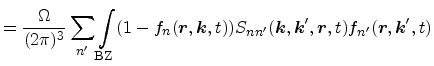
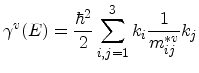
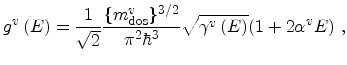
![$\displaystyle m^v_\mathrm{dos}= \sqrt[3]{ \{m^*_{11}\}^v \{m^*_{22}\}^v \{m^*_{33}\}^v } \ ,%\vphantom{\sum_i}
$](img872.png)
![]() ) to state (
) to state (
![]() ) for phonon
scattering in a non-polar semiconductor can be written as [Jacoboni83]
) for phonon
scattering in a non-polar semiconductor can be written as [Jacoboni83]