| (2.99) | |
| (2.100) | |
| (2.101) |
This section gives an overview about the steady-state and transient simulation modes including a discussion of the nonlinear solution technique. For the steady-state analysis, the discretized equations (2.21), (2.22), and (2.23) can be symbolically written as:
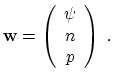 |
(2.102) |
Note that for the sake of simplification, the vectors of the discretized quantities and equations are not explicitly noted. The resulting discretized problem is then usually solved by a damped Newton method which requires the solution of a linear equation system at each step. The result of the steady-state simulation mode is the operating point, which is a prerequisite for any subsequent transient or small-signal simulation.
As the resulting discretized equation system is still nonlinear, the solution
![]() , which is assumed to exist is obtained by applying a linearization
technique. The nonlinear problem can be defined as
, which is assumed to exist is obtained by applying a linearization
technique. The nonlinear problem can be defined as
| (2.103) |
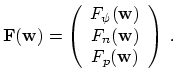 |
(2.104) |
Then,
![]() is a so-called contractive mapping, and the locally
convergent iteration does converge for any
is a so-called contractive mapping, and the locally
convergent iteration does converge for any
![]() to
to
![]() . In order to
fulfill (2.105) it is assumed that the Frechet
derivative
. In order to
fulfill (2.105) it is assumed that the Frechet
derivative
![]() exists at the fixpoint
exists at the fixpoint
![]() and that its eigenvalues
are less than one in modulus [193]. According to the
Ostrowski theorem [243],
and that its eigenvalues
are less than one in modulus [193]. According to the
Ostrowski theorem [243],
![]() is contractive if
the spectral radius
is contractive if
the spectral radius
![]() , which is the maximal modulus of
all eigenvalues of
, which is the maximal modulus of
all eigenvalues of
![]() . If
. If
![]() exists such that
exists such that
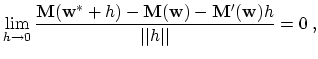 |
(2.106) |
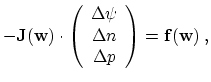 |
(2.107) |
| (2.109) |
It is important to note that
![]() must only be an approximation of the
Frechet derivative, which follows from the derivation of
must only be an approximation of the
Frechet derivative, which follows from the derivation of ![]() [193]. Furthermore, in order to enlarge the radius of convergence and
thus improve the convergence behavior of the Newton approximation,
the couplings between the equations can be reduced, especially during the first
steps of the iteration. Before the update norm, that is the infinity norm of
the update vectors of all quantities, has fallen below a specified value, the
derivatives as shown in Table 2.1 are normally ignored. Besides the
driving force for electrons and holes in the drift-diffusion model,
[193]. Furthermore, in order to enlarge the radius of convergence and
thus improve the convergence behavior of the Newton approximation,
the couplings between the equations can be reduced, especially during the first
steps of the iteration. Before the update norm, that is the infinity norm of
the update vectors of all quantities, has fallen below a specified value, the
derivatives as shown in Table 2.1 are normally ignored. Besides the
driving force for electrons and holes in the drift-diffusion model, ![]() and
and
![]() , and the tunneling current density
, and the tunneling current density
![]() , all quantities are already
known from the previous sections. Note that for the sake of simplification just
the symbols are given without vector notations.
, all quantities are already
known from the previous sections. Note that for the sake of simplification just
the symbols are given without vector notations.
The linear equation system for the ![]() -th iteration step looks like:
-th iteration step looks like:
| (2.110) |
| (2.111) |
| (2.112) |
The transient problem arises if the boundary condition for the electrostatic potential or the contact currents becomes time-dependent. Hence, the partial time derivatives of the carrier concentrations in (2.22) and (2.23) have to be taken into account.
There are several approaches for transient analysis [193], among them
are the forward and backward Euler approaches. Whereas the former
shows significant stability problems, the latter is unconditionally stable for
arbitrarily large time steps ![]() .
However, full backward time differencing
requires much computational resources for solving the large nonlinear
equation system at each time step, but gives good results.
The quality of the results can be measured by the truncation error
[146]. Equations (2.21), (2.22) and
(2.23), discretized in time and symbolically written, read then at the
.
However, full backward time differencing
requires much computational resources for solving the large nonlinear
equation system at each time step, but gives good results.
The quality of the results can be measured by the truncation error
[146]. Equations (2.21), (2.22) and
(2.23), discretized in time and symbolically written, read then at the
![]() -th time step when
-th time step when ![]() is to be calculated:
is to be calculated:
| (2.114) | |
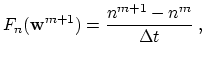 |
(2.115) |
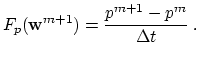 |
(2.116) |
From a computational point of view it is to note, that in comparison to the steady-state solution the algebraic equations arising from the time discretization are significantly easier to solve [193]. This has mainly two reasons: first, the partial time derivatives help to stabilize the spatial discretization. Second, the solutions can be used as a good initial guess for the next time step. Furthermore, the equation assembly structures can be reused (see Section 4.12).