In the following, different algorithms for tetrahedral mesh adaptation are developed to fulfill state-of-the-art demands of TCAD simulations. First some definitions of commonly used technical terms have to be given, to provide the non-experienced reader with some convenient descriptions. Slightly different definitions can be found in literature, but the following ones are in the style of explanations given in [4].
For example, a 0-simplex is a point, a 1-simplex is a line segment, a 2-simplex
is a triangle, a 3-simplex is a tetrahedron, and a 4-simplex is a pentachoron,
also known as pentatope (in each case with interior) in its adequate dimension.
A tetrahedron is a polyhedron composed of four triangular faces, three of which
meet at each vertex. A regular tetrahedron is one in which the four triangles
are regular, or "equilateral", and is one of the Platonic solids. A
tetrahedron is referred as a 3-simplex.
| (2.2) | |||
| (2.3) | |||
| (2.4) | |||
| (2.5) |
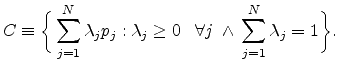 |
In ![]() dimensions, the gift wrapping algorithm [33], which has
complexity
dimensions, the gift wrapping algorithm [33], which has
complexity
![]() , where
, where
![]() is the
floor function, can be used. In two and three dimensions,
however, specialized algorithms exist with complexity
is the
floor function, can be used. In two and three dimensions,
however, specialized algorithms exist with complexity
![]() .
.
Let ![]() be a (finite) set of points in
be a (finite) set of points in ![]() (
(
![]() ), the convex
hull of
), the convex
hull of ![]() , denoted as
, denoted as
![]() , defines a domain
, defines a domain ![]() in
in
![]() . Let
. Let ![]() be a simplex, then the covering up
be a simplex, then the covering up
![]() of
of
![]() by means of such elements corresponds to the following:
by means of such elements corresponds to the following:
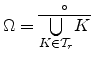 , where
, where
Here is a natural definition: with respect to condition ![]() , one can
see that
, one can
see that ![]() is the open set corresponding to the domain that means, in
particular, that
is the open set corresponding to the domain that means, in
particular, that
![]() . Condition
. Condition ![]() is not strictly necessary to define a covering up, but it
is nevertheless practical with respect to the context and, thus, will be
assumed. Condition
is not strictly necessary to define a covering up, but it
is nevertheless practical with respect to the context and, thus, will be
assumed. Condition ![]() means that element overlapping is proscribed [4].
means that element overlapping is proscribed [4].
Let ![]() be a closed bounded domain in
be a closed bounded domain in ![]() (
(
![]() ). The
question is how to construct a confirming triangulation of this domain. Such a
triangulation will be referred to as a mesh of
). The
question is how to construct a confirming triangulation of this domain. Such a
triangulation will be referred to as a mesh of ![]() and will be
denoted by
and will be
denoted by
![]() .
.
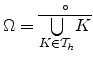 .
.
In contrast, Definition 5-![]() is no longer assumed, which means that the vertices are not in general, given
a priori and in Definition 7-
is no longer assumed, which means that the vertices are not in general, given
a priori and in Definition 7-![]() , the
, the ![]() s are not
necessarily simplices.
s are not
necessarily simplices.
Most computational schemes using a mesh as a spatial support assume that this mesh is conformal (although, this property is not strictly necessary for some solution methods).
Elements are the basic components of a mesh. An element is defined by its geometric nature and a list of vertices.