Subsections

• 2.3.1 Anisotropic Metric
  • 2.3.1.1 Exemplification
  
  
• 2.3.2 Anisotropic Tetrahedral Bisection

2.3 Anisotropy

In common, anisotropy is understood as the condition of holding a property value being dependent on the directions in which it is observed. For better understanding of the term anisotropy in the context of tetrahedral meshes first a definition for mesh density is given. Second, a novel approach is presented of how anisotropy can be seen as property of a single tetrahedron and how this property can be visualized. Afterwards an extension of the recursive tetrahedral bisection algorithm, presented in Section 2.2.3, is depicted, which can largely benefit from the incorporation of an anisotropic metric.

Definition 12 (Mesh density)   defines an average number of geometric objects per unit volume. For geometric objects typically 0 -simplices (see Section 2.1.1) or mesh elements (see Section 2.1.9) are used, but also others are possible.

In general anisotropy in context of tetrahedral meshes can be seen as direction-dependent variation of mesh density (see Definition 12). Mapping this idea on a tetrahedron, anisotropy can be understood as variation of the coordinate system related distances between the vertices. This thought is based on a method which is a well-known statistical technique called Principal Component Analysis (PCA) [46]. PCA is a useful method that has found application in many scientific areas, such as, image analysis and compression, face recognition, and regression. PCA is also a common technique for finding patterns in data of high dimensions [47].

Appendix A gives a full representation on how PCA is used to find a quantitative description for the geometric property of a tetrahedron. However, PCA analysis for a tetrahedron forms a quadratic surface which can be used as measure for anisotropy, i.e. roughly speaking if PCA comes up with a sphere the tetrahedra is more regular (isotropy). If it forms an ellipsoid, than the tetrahedron is said to be anisotropic, see Figure 2.5.

Figure 2.5: Anisotropic property of a tetrahedron can be understood as variation of the coordinate system related distances between the vertices. Principal Component Analysis (PCA) applied to a tetrahedron forms a symmetric $3 \times 3$ covariance matrix. The eigensystem of the covariance matrix constitutes a quadratic surface which is used for visualization. Figure 2.5(a) and Figure 2.5(b) give the orthogonal eigenvectors scaled by the eigenvalues (red arrows) and the according quadratic surface (transparent blue hull) for a geometrically distorted and a regular tetrahedron, respectively.

In the following it is shown, how regular, mostly isotropic meshes can be transformed by refinement into anisotropic meshes. The idea is based on the introduction of a tensor-based metric space, representing mesh anisotropy over the domain [48], which controls a modified tetrahedral bisection algorithm.

2.3.1 Anisotropic Metric

Based on the ideas discussed in Section 2.3 we want to go the other way around and start with a definition of the term metric and how a tensor function can be used to form a non-constant anisotropic metric space.

Definition 13 (Metric)   A non-negative function $g(x,y)$ describing the distance between neighboring points for a given set. A metric satisfies the triangle inequality

$$g(x,y) + g(y,z) \geq g(x,z)$$

and is symmetric

$$g(x,y) = g(y,x).$$

A metric also satisfies

$$g(x,x) = 0,$$

as well as the condition that

$$g(x,y) = 0, \quad x \equiv y.$$

If the latter condition is dropped, then $g(x,y)$ is called pseudo-metric instead of metric. A set possessing a metric is called a metric space. When viewed as a tensor, the metric is called a metric tensor [49,50].

For a better understanding of the following I also want to give a definition for a metric tensor [51].

Definition 14 (Metric Tensor)   is a tensor $\mathbf{M}=(m_{i,j})$ , also called Riemannian metric, which is symmetric and positive definite. Its components can be viewed as multiplication factors which must be placed in front of the differential displacements $d x_i$ in a generalized Pythagorean theorem

$$ds^2=m_{11}dx_{1}^2 + m_{12}dx_{1}dx_{2}+m_{22}dx_{2}^2+\cdots.$$

In Euclidean space, $m_{i,j} = \delta_{i,j}$ where $\delta$ is the Kronecker delta (which is 0 for $i \neq j$ and $1$ for $i=j$ ), reproducing the usual form of the Pythagorean theorem

$$ds^2=m_{11}dx_{1}^2 +m_{22}dx_{2}^2+\ldots.$$

In the following the anisotropic metric $\mathbf{M}$ is a tensor function that varies over the domain $\mathbf{M}=\mathbf{M}(x,y,z)$ .

Applying this metric to tetrahedral meshes means that calculating the edge length of an element in a metric space can be seen as calculating a line integral. An arc length $\ell_{C}$ is defined as the length along a curve $C$ : $\ell_{C}= \int_{C} \; ds$ . The length of a line segment $\overline{PQ}$ in a metric space is calculated by

$$\ell_{PQ}=\int_{0}^{1}\sqrt{\overline{PQ}^{T} \cdot \mathbf{M}(P+t\cdot\overline{PQ}) \cdot \overline{PQ}}\:dt$$ (2.6)

where $\mathbf{M}(P+t\cdot\overline{PQ})$ is the metric at point $P+t\cdot\overline{PQ}$ , $t\in [0,1]$ .

The idea now is to apply a combination of coordinate system rotation $(x,y,z) \mapsto (\xi,\eta,\zeta)$ (see Appendix B.1) and dilation defining the anisotropic metric function $\mathbf{M}=\mathbf{M}(x,y,z)$ , where the dilation is represented by three scalar values $\lambda_{\xi},\lambda_{\eta},$ and $\lambda_{\zeta}$ , respectively.

Using $(\vec{\xi},\vec{\eta}, \vec{\zeta})$ as an orthogonal coordinate system and the dilation values $(\lambda_{\xi},\lambda_{\eta},\lambda_{\zeta})$ we define two matrices

$$\mathbf{R}:= \begin{pmatrix}\xi_{x} & \eta_{x} & \zeta_{x} \ \xi_{y} & \eta_{y} & \zeta_{y} \ \xi_{z} & \eta_{z} & \zeta_{z} \end{pmatrix} \mathbf{S}:= \begin{pmatrix}\lambda_{\xi} & 0 & 0 \ 0 & \lambda_{\eta} & 0 \ 0 & 0 & \lambda_{\zeta} \end{pmatrix}.$$ (2.7)

Combining matrices $\mathbf{R}$ and $\mathbf{S}$ gives a $3\times{}3$ positive definite matrix

$$\mathbf{M}:=\mathbf{R} \mathbf{S} \mathbf{R}^{T}$$ (2.8)

which describes three-dimensional anisotropy.

In general a tensor $\mathbf{M}=(m_{ij})$ formed by a $3 \times 3$ matrix can be split into a symmetric $\mathbf{M}^s = (m_{ij}^s)$ and an antisymmetric part $\mathbf{M}^a=(m_{ij}^a)$ such that $\mathbf{M} = \mathbf{M}^s + \mathbf{M}^a$ where $(m_{ij}^s) = \frac{1}{2}(m_{ij}+m_{ji})$ and $(m_{ij}^a) = \frac{1}{2}(m_{ij}-m_{ji})$  [52]. The antisymmetric part in essence describes a rotation merely, so the following deals with symmetric, second order tensors only.

2.3.1.1 Exemplification

According to matrix $\mathbf{R}$ and matrix $\mathbf{S}$ the metric tensor can be seen as three-dimensional distortion of a sphere. For example, in a simple case, where the rotation matrix $\mathbf{R}$ is equal to the identity matrix $\mathbf{R}\equiv \mathbf{I}$ and the distortion matrix is set as

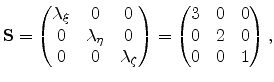$$\mathbf{S}= \begin{pmatrix}\lambda_{\xi} & 0 & 0 \ 0 & \lambda_{... ...nd{pmatrix} = \begin{pmatrix}3 & 0 & 0 \ 0 & 2 & 0 \ 0 & 0 & 1 \end{pmatrix},$$ (2.9)

an initial sphere is transformed to an ellipsoid, which represents the new metric (compared to the undistorted Euclidean metric) measurement units of the distorted space. This point of view is depicted in Figure 2.6 and Figure 2.7, respectively.

For the visualization of pointwise defined second order tensor functions a so-called glyph-based, more exactly, a metric ellipsoids glyph-based approach [53] is used which is described in detail in Appendix A.3.

In Figure 2.7 one can see, that there is no distortion along the $z$ -axis. In the $x$ -direction the space is stretched by a factor of three and in $y$ -direction by a factor of two. According to formula (2.2) the square length of an edge $\ell_{PQ}^2$ which is oriented exactly $x$ -directional appears three times longer then the same edge measured in an undistorted Euclidian space (where the metric tensor function $\mathbf{M}$ is equal to the identity matrix $\mathbf{M} \equiv \mathbf{I}$ ).

In this simplified case the rotation matrix was set to the identity matrix $\mathbf{I}$ and therefore, the distorted space and the undistorted space are collateral. Please notice that the metric tensor function in this example does not vary over the space and is therefore constant: $\mathbf{M}=\mathbf{M}(x,y,z) = \operatorname{const}$ .

Figure 2.6: Metric representation for an isotropic Euclidian space, where the metric tensor function is set to the identity matrix $\mathbf{M}=\mathbf{M}(x,y,z) = \mathbf{I}=\operatorname{const}$ .

Figure 2.7: Metric representation for an anisotropic distorted space, where for exemplification the metric tensor function $\mathbf{M} = \mathbf{M}(x,y,z) = (3,2,1)^T \cdot \mathbf{I} = \operatorname{const}$ was chosen. The sphere depicted in Figure 2.6 is transformed to an ellipsoid.

2.3.2 Anisotropic Tetrahedral Bisection

With the help of the anisotropy metric function defined in Section 2.3.1 and the bisection algorithm presented in Section 2.2.2, an anisotropic tetrahedral bisection algorithm can be derived.

The basic idea behind this refinement procedure is to calculate the length of all edges marked for refinement in a given metric and to determine the longest anisotropic edge according to the metric function through formula (2.2). Afterwards, the longest anisotropic edge is cut into two pieces of equal (isotropic measured) length. During this cutting process all new edges must also be taken into consideration. Now the procedure starts again by marking edges according to the refinement criterion and stops if there is no edge which fulfills the criterion anymore. Table 2.2 gives a pseudo-code fragment which shows the nature of this algorithm.

Table 2.2: Algorithm; Anisotropic tetrahedral bisection.

The complexity of the algorithm depends mostly on the amount of edges produced during the cutting process. This is in general unknown and can only be calculated exactly subsequently. Under the assumptions that the initial mesh carries $n$ -edges, $k$ -edges are marked for refinement, and $x$ -edges are born during the overall refinement process, the complexity has the bounded order of $\mathcal{O}(n + k \log_2 k + x \log_2 x)$ .

One open item is the RefinementCriterion-function used in the anisotropic tetrahedral bisection algorithm, depicted in Table 2.2. One has to distinguish between pure geometric RefinementCriterion-functions and so-called data driven RefinementCriterion-functions which are subject of Section 3. Pure geometric RefinementCriterion-functions come to a decision only by analyzing geometric properties of the refinement edge and all associated mesh elements. The recursive tetrahedral bisection algorithm presented in Section 2.2.3 is a member of this class.

The simplest case for a RefinementCriterion-function under consideration of a given metric function is shown in Table 2.3. In this particular case the length of the refinement edge is calculated related to a given MetricFunction $\mathbf{M}=\mathbf{M}(x,y,z)$ with respect to Equation (2.2). As second step a maximum edge length limit is introduced, which bounds the anisotropic length of each edge. If the length exceeds the limit, the edge is marked for refinement otherwise not.

Table 2.3: Algorithm; Refinement criterion function.

Strictly speaking this RefinementCriterion-function is already a data driven refinement method, because the metric function itself is analyzed for the refinement decision and so not only pure geometric properties are used. However, in Section 3 different data driven RefinementCriterion-functions are derived, which enables a powerful anisotropic mesh refinement technique for several simulation tasks for TCAD tools.