


Next: 5.3 Example
Up: 5. Dynamic Mesh Adaptation
Previous: 5.1 Electromigration in a
Subsections
5.2 Interface Mesh Modeling
Interfaces understood as a common boundary between two or more substances
occur in a wide variety of settings. We distinguish between static and
dynamic interfaces, where in the first case borders do not change over
time and in the latter case are somehow time dependent. Dynamic interfaces are
also called propagating interfaces, which implies the movement or more
general also the formation, partition, assembly, and disappearance of
interfaces over time.
In 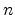 dimensional space
dimensional space
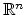 the dimension of the interface is
the dimension of the interface is 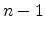 ,
which means that the interface has codimension one [88,89]. For three
spatial dimensions
,
which means that the interface has codimension one [88,89]. For three
spatial dimensions
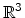 , which is the mostly used case in this
thesis, the lower-dimensional interface is a two-dimensional surface embedded
in
, which is the mostly used case in this
thesis, the lower-dimensional interface is a two-dimensional surface embedded
in
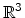 . Under consideration of a simplified matter
one can say that an interface separates
. Under consideration of a simplified matter
one can say that an interface separates
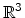 into distinct
sub domains with nonzero volume. Degenerated cases where the interface is of
higher codimension are neglected in aid of a clear and simple picture of
interfaces.
into distinct
sub domains with nonzero volume. Degenerated cases where the interface is of
higher codimension are neglected in aid of a clear and simple picture of
interfaces.
The following deals with three-dimensional material boundaries
which occur e.g. during the formation of
voids in interconnect lines. Two different main interface modeling approaches,
namely the explicit interface and the
implicit interface are presented in detail and their reflection on the
resulting meshing demand is discussed on a propaedeutic example. A variation
of an implicit interface, the so-called diffuse interface, is subject of
the interface modeling section used for the simulation of electromigration. This
interface needs special mesh treatments which yield the refined diffuse
interface.
Figure 5.2:
Illustration of an intersection between a sphere (blue) and a
cube (red). The intersection plane (yellow) of these solids forms an interface
which is part of further discussions.
![\begin{figure*}\setcounter{subfigure}{0}
\mbox{\subfigure[Perspectivic view.]
{...
...fig{figure =pics/EM-cube-sphere-top.eps2,width=0.49\textwidth}}}
\end{figure*}](img359.png) |
In the following
illustration the interface is defined as the intersection of a sphere and a cube,
where the center of the sphere is identical with one vertex of the
cube. In Figure 5.2 a perspectivic and the according top view of
these two solids and their intersection plane are shown. The intersection plane
(yellow) cuts away a globular part near the center point of the sphere (blue)
from the cube (red) and an interface, a borderline between the sphere and the
cube, occurs. This interface is subject of the following two different modeling
approaches in context with three-dimensional tetrahedral based meshes as
spatial tessellation of the solids.
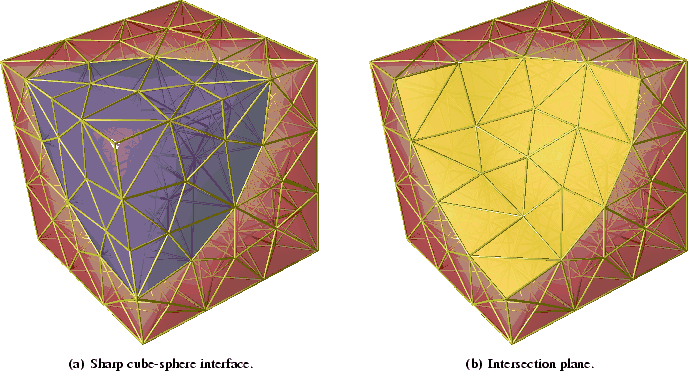
Figure 5.3:
Illustration of an intersection between one quarter of a
sphere (blue) and a cube (red). The intersection plane (yellow) of these solids
forms an interface which is part of the tetragonal tessellation and therefore
called sharp interface or explicit interface.
 |
Sine qua non of this approach is that an arbitrary interface
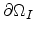 given as intersection of domain boundaries
given as intersection of domain boundaries
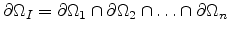 of regions
of regions
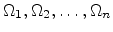 is
integral part of the spatial tessellation. In other words, if
is
integral part of the spatial tessellation. In other words, if
 is
the discretized representation of the volumetric domain
is
the discretized representation of the volumetric domain 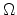 with a hull
given by
with a hull
given by
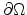 , then
, then
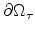 must be part of
must be part of
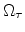 , i.e.
, i.e.
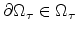 .
.
As noticed in Section 5.2, if the spatial dimension of the interface
has codimension one then the interface is one dimension lower than the dimension of
the space region, i.e. for
three-dimensional volumetric contacting regions the interface is a
two-dimensional surface embedded in three-dimensional space. This is in
general also valid for the discrete representation of a spatial domain given by a
mesh and for the used mesh elements itself.
In some exceptional cases the
interface can also be of higher codimension, i.e. that the dimension of the
interface is lower than 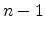 for an
for an 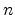 -dimensional region. That is
the case, if several three-dimensional regions share only one common
point. Then the interface has codimension two and not one. This exception does not
carry much authority and can be easily handled by discrete region
representations.
-dimensional region. That is
the case, if several three-dimensional regions share only one common
point. Then the interface has codimension two and not one. This exception does not
carry much authority and can be easily handled by discrete region
representations.
By the choice of a discrete interface representation on a three-dimensional
tetrahedron based mesh, the interface itself is given by a set of triangles and
their associated edges and points which are compulsory parts of the mesh
elements. Figure 5.3 illustrates such a sharp interface for an
introductive example. The interface is defined by the set of all yellow
triangles depicted in Figure 5.3(b).
If the mesh is a conformal mesh, as defined in Section 2.1.8, then the
interface must also be conformal. This means for our example, that
the sphere and the cube can be glued together, and the union forms a
conformal mesh again.
The advantage of sharp interfaces is their clear representation through
geometric elements. For the three-dimensional tessellation based on unstructured
tetrahedron meshes the interface can be defined by a set of triangles, edges,
and points as depicted in Figure 5.3. Sharp interfaces are a good
choice for static interfaces.
In the dynamic case a disproportional effort has
to be undertaken to guarantee a conformal mesh for propagating interfaces,
since the connectivity can change. The interface must be resolved over and over
again for every time step. One very critical issue is to check, if interfaces
merge together or pinch apart, because this causes special
treatments and difficulties including, for example, determination of holes in
the surface. One can imagine that the reorganization of such interfaces involves
complicated remeshing procedures which are difficult to handle. This all gives
motivation for another interface representation which is more suitable for
dynamic interfaces, the group of so-called implicit
interfaces.
5.2.2 Implicit Interface
The term implicit interface has
its origin in the wide field of analytic geometry which is the area of
mathematics that deals with the relation between geometry and mathematical
expressions of coordinates of points in space. When applied to
three-dimensional space, it is called solid analytic
geometry [88,90]. The essential element of this mathematical field is a
function which describes a geometric object.
For example, an explicit
equation might express the 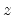 -coordinate in terms of the
-coordinate in terms of the 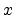 and
and 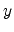 coordinates; that is
coordinates; that is 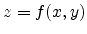 . Such a surface is called height
field. Explicit representations show strong limitations in respect of the
shape of the surface. It is not possible to describe closed
surfaces with an explicit surface representation.
. Such a surface is called height
field. Explicit representations show strong limitations in respect of the
shape of the surface. It is not possible to describe closed
surfaces with an explicit surface representation.
One approach is to use a parametric representation. For a
two-dimensional surface embedded in three-dimensional space, this leads to
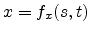 ,
,
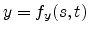 , and
, and
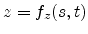 . The other approach in which we
are more focused is implicit: the coordinates are treated as functional
arguments rather than functional values.
. The other approach in which we
are more focused is implicit: the coordinates are treated as functional
arguments rather than functional values.
Usually surfaces are presented via,
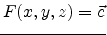 , where
, where 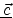 is a point
in
is a point
in
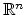 and
and 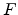 maps
maps
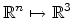 . For most
applications,
. For most
applications, 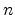 is
is 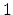 and
and 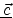 is a scalar. If
is a scalar. If 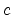 is zero, we say
that
is zero, we say
that 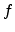 implicitly defines a locus called an implicit surface; that is,
the set of points
implicitly defines a locus called an implicit surface; that is,
the set of points
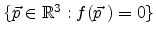 is a
surface implicitly defined by
is a
surface implicitly defined by 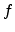 . The function
. The function 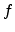 is called implicit
surface function or a scalar field, a field function, or a potential
function. The implicit surface is sometimes called the zero set of
is called implicit
surface function or a scalar field, a field function, or a potential
function. The implicit surface is sometimes called the zero set of 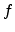 and may be written as
and may be written as 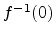 or
or 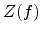 . The according
iso-surface (also called a level set or level surface) is
. The according
iso-surface (also called a level set or level surface) is
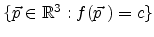 , where
, where 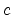 is the
iso-contour value of the surface [91,92].
is the
iso-contour value of the surface [91,92].
For more sophisticated surfaces without analytical representation, we need to use a
discretization. This means, 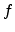 can be seen as a pointwise sampled function
according to the points of a three-dimensional mesh where each vertex holds a value
of
can be seen as a pointwise sampled function
according to the points of a three-dimensional mesh where each vertex holds a value
of 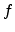 . To get a smooth representation of
. To get a smooth representation of 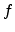 all over the
three-dimensional domain, an interpolation scheme for function
values between the sampling points is used.
all over the
three-dimensional domain, an interpolation scheme for function
values between the sampling points is used.
In this work a linear basis function interpolation scheme was used which is very
common in the field of finite element calculations as discussed in
Section 3.1.3. The exact position of the interface is now determined by
the chosen interpolation scheme and the mesh density, whereby the latter can be
influenced by appropriate mesh adaptation techniques.
Figure 5.4:
Implicit interface representation between the sphere and the cube. Due
to the usage of linear interpolation between the mesh points, the interface
defined by Equation (5.3) smears out. A cross cut through the
mesh structure and level surfaces are plotted for iso-contour values 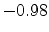 (blue),
(blue), 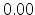 (green) , and
(green) , and 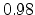 (red) in the right picture.
(red) in the right picture.
 |
Back to the illustration example,
Figure 5.4 shows the implicit interface representation between the
sphere and the cube. A sphere with radius 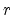 and center point
and center point
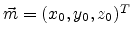 can be implicitly written as:
can be implicitly written as:
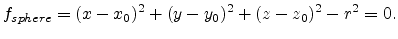 |
(5.2) |
In this particular case the sphere-cube interface function with respect
to (5.2) is defined similar to a Heaviside
function [93]:
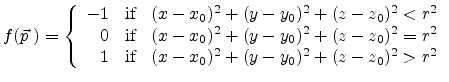 |
(5.3) |
where for the example, 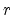 was set to
was set to 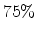 of the side length of the cube. The
evaluation of the interface definition given by Equation (5.3) for
every vertex of an existing mesh for the cube yields Figure 5.4(a),
where the coloration mirrors the values of
of the side length of the cube. The
evaluation of the interface definition given by Equation (5.3) for
every vertex of an existing mesh for the cube yields Figure 5.4(a),
where the coloration mirrors the values of
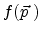 . A linear
interpolation scheme was used for the evaluation of function points between the
three-dimensional sampling points.
. A linear
interpolation scheme was used for the evaluation of function points between the
three-dimensional sampling points.
Due to the linear interpolation scheme and an unstructured tetrahedron based mesh
the Heaviside function smears out and a wider interface region appears than
initially defined by (5.3). Figure 5.4(b) shows
level surfaces for the iso-contour values 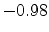 (blue),
(blue), 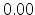 (green), and
(green), and
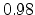 (red).
(red).
Numerical interpolation produces an error in the estimation of 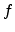 . This can lead
to perturbing or moving the interface away from its exact position. If these
interface perturbations are small, their effects may be minor and a perturbed
interface might be acceptable. In general, most numerical methods depend on the
fact that their results are stable in the presence of small perturbations. If this
is not true, then the problem under consideration is probably ill-posed and
numerical methods should be used with extreme caution. These interface
perturbation errors decrease as the number of sample points increases, implying
that the exact answer could hypothetically be computed as the number of sample
points is increased to infinity, which is the basis for most numerical
methods [94].
. This can lead
to perturbing or moving the interface away from its exact position. If these
interface perturbations are small, their effects may be minor and a perturbed
interface might be acceptable. In general, most numerical methods depend on the
fact that their results are stable in the presence of small perturbations. If this
is not true, then the problem under consideration is probably ill-posed and
numerical methods should be used with extreme caution. These interface
perturbation errors decrease as the number of sample points increases, implying
that the exact answer could hypothetically be computed as the number of sample
points is increased to infinity, which is the basis for most numerical
methods [94].
It seems unlikely that any standard numerical approximation based on sampling
will give a good approximation to a Heaviside like function. A wide range of
smooth approximations of the Heaviside function are in use, which are
commonly defined by limits. In the following three examples of such definitions
are given, further definitions can be found e.g. in [95,96].
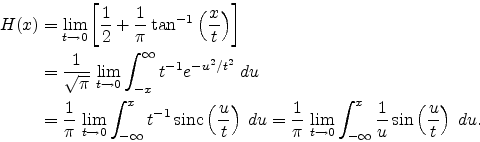 |
(5.4) |
For the simulation of void migration in interconnect lines, a special
representation of an implicit interface function is used, where the interface
width itself is varied. This interface is part of the following.
A special kind of implicit interfaces is the so-called diffuse interface
which is driven by the modeling of void migration and void growth due to bulk
diffusion. This particular interface representation
is mostly governed by the Cahn-Hilliard equation [97] where the void
structure is described by an order parameter field,
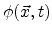 that separates the interconnect line into a material phase
and a void phase with a thin interface between them. The structure of the
interface model equations in an unpassivated interconnect line can be written
as
that separates the interconnect line into a material phase
and a void phase with a thin interface between them. The structure of the
interface model equations in an unpassivated interconnect line can be written
as
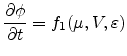 with with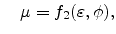 |
(5.5) |
where 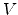 is the electrical potential,
is the electrical potential, 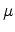 denotes the chemical potential,
and
denotes the chemical potential,
and
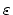 is a parameter controlling the void-metal
interface [98,99].
is a parameter controlling the void-metal
interface [98,99].
The used one-dimensional interface definition function in the value range from 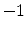 to
to 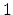 reads:
reads:
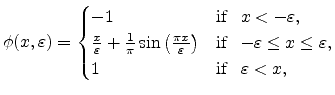 |
(5.6) |
where
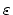 determines the size of numerical
smearing. In [94] a rule of thumb gives a value of
determines the size of numerical
smearing. In [94] a rule of thumb gives a value of
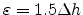 for the tuning parameter on a uniform grid with a constant spacing
of
for the tuning parameter on a uniform grid with a constant spacing
of 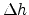 . This makes the interface width equal to three grid
cells. Figure 5.5 shows a one-dimensional interface definition
function, cf. Equation (5.6), with emphasis on different
values for the tuning parameter
. This makes the interface width equal to three grid
cells. Figure 5.5 shows a one-dimensional interface definition
function, cf. Equation (5.6), with emphasis on different
values for the tuning parameter
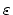 .
.
Figure 5.5:
Tunable one-dimensional interface definition function.
|
|
An increase of
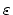 causes a wider interface and increases numerical
stability, but too flat transitions should also be avoided due to the
loss of
accuracy in the iso-level finding procedure. This problem is comparable with
finding an intersection point of two straight line segments with a very small
intersection angle [100].
Turning
causes a wider interface and increases numerical
stability, but too flat transitions should also be avoided due to the
loss of
accuracy in the iso-level finding procedure. This problem is comparable with
finding an intersection point of two straight line segments with a very small
intersection angle [100].
Turning
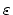 close to zero gives a very sharp transition which
defines a clear boarder but can lead to numerical instability in the face of
spatial sampling.
close to zero gives a very sharp transition which
defines a clear boarder but can lead to numerical instability in the face of
spatial sampling.
One way to increase spatial resolution and therefore numerical accuracy is to
use a finer mesh all over the domain. Driving this idea to an extreme
yields an infinite number of mesh points with a maximum on possible
numerical accuracy.
The drawback of course is also infinite high computational expenses
on both, calculating time and memory usage. To bear down this problem
a third form, a mixed form between fine and coarse mesh is used. Since the
interface uses only a small part of the whole mesh domain, one can increase the
spatial resolution only in a small area surrounding the interface itself, which
yields the so-called refined diffuse interface.
Figure 5.6 shows the same interface as presented in
Figure 5.4, but now with an isotropic refined interface belt. For
the zoning of the refinement procedure the three-dimensional extension of the
interface function definition as depicted in Equation (5.6) itself
can be used.
The tuneable parameter
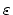 is now also responsible for the refinement
procedure, i.e. that only elements within the
is now also responsible for the refinement
procedure, i.e. that only elements within the
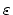 -environment
-environment
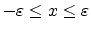 are used for refinement. In this example
an isotropic recursive refinement approach as described in Section 2.2.3
was used only for elements within the refinement belt, which forms mostly
isotropic elements. Elements outside the belt are untouched and, therefore,
almost not involved in the refinement process.
are used for refinement. In this example
an isotropic recursive refinement approach as described in Section 2.2.3
was used only for elements within the refinement belt, which forms mostly
isotropic elements. Elements outside the belt are untouched and, therefore,
almost not involved in the refinement process.
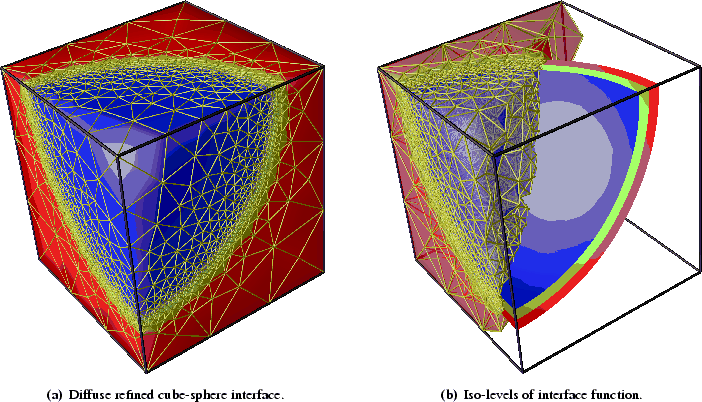
Figure 5.6:
Diffuse refined interface representation between the sphere and
the cube. A refined region surrounds the interface with higher mesh density
and, therefore, a higher numerical accuracy is reached. A cross cut through the
mesh structure and level surfaces are plotted for iso-contour values
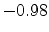 (blue),
(blue), 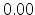 (green) , and
(green) , and 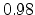 (red) in the right picture.
(red) in the right picture.
 |
Due to the nature of the recursive approach the spatial zoning is not always
guaranteed and influences possibly also regions outside of the interface zone.
Another disadvantage is also the necessity of tracing the interface in the case
of a dynamic
interface. After each time step the interface propagates and, therefore, the
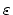 -environment becomes also time dependent, i.e. the refinement
procedure has to observe the interface. If the interface moves into new
regions which are previously untouched, they have to be refined.
-environment becomes also time dependent, i.e. the refinement
procedure has to observe the interface. If the interface moves into new
regions which are previously untouched, they have to be refined.
On the one hand side this tracking guarantees always a good resolution of the
interface, on the other hand side it slows down the simulation, because only new
points are added. Old ones which are run out of the interface zone remain still
present.
Remediation of this matter is performed with the so-called hierarchical mesh
refinement-coarsement scheme which is part of the next section.
5.2.5 Hierarchical Mesh Refinement-Coarsement Scheme
According to the demands of void movement simulation during electromigration also a
mesh coarsening step has to be introduced. In analogy to the term ``refinement'',
the coarsening procedure was named coarsement. The basic idea behind
this coarsement strategy is that a previous refinement step is reversed. This
procedure can be handled easily by introducing a hierarchical element structure
as shown in Figure 5.7 and is therefore called hierarchical
mesh refinement-coarsement scheme.
Figure 5.7:
Data structure of a hierarchical refinement-coarsement scheme.
|
|
During transient simulation the position of the interface belt is detected
after each timestamp and the mesh resolution is controlled. Too coarse elements
are refined by recursive tetrahedral bisection. Regions which have been refined
in a previous step and which are not covered by the void-metal interface any
longer, are loaded into the coarsement module. Due to the properties of the
hierarchical element data structure, the initial (before refinement) mesh
constellation can be recovered easily.
It is in the nature of this approach that the initial mesh is always a subset
of the current mesh and no coarser mesh than the initial one can be
reached. This seems to be a handicap, however, the coarsest mesh is
defined by the initial one and therefore the lowest spatial resolution is known,
which controls the numerical error introduced by the starting
mesh [101].



Next: 5.3 Example
Up: 5. Dynamic Mesh Adaptation
Previous: 5.1 Electromigration in a
Wilfried Wessner: Mesh Refinement Techniques for TCAD Tools
![\begin{figure*}\setcounter{subfigure}{0}
\mbox{\subfigure[Perspectivic view.]
{...
...fig{figure =pics/EM-cube-sphere-top.eps2,width=0.49\textwidth}}}
\end{figure*}](img359.png)


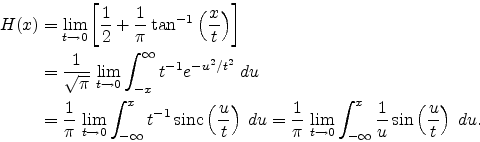
 with
with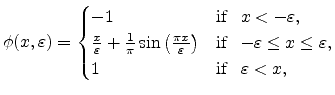
![\includegraphics[width=0.75\textwidth]{pics/InterfaceFunction.eps}](img397.png)

![\includegraphics[width=0.63\columnwidth,height=0.48\columnwidth]{pics/hierarchy}](img400.png)