Clemens Etl Dipl.-Ing. Publications

Biography Clemens Etl was born in Wr. Neustadt, Austria, in 1990. He studied Technical Mathematics at the TU Wien where he received his master's degree in 2019. After graduation, he worked as a scientific assistant in the field of artificial intelligence at the Know-Center in Graz. He joined the Institute for Microelectronics in May 2022 where he is currently working on his doctoral degree. He is researching high performance electron quantum transport modeling and simulation approaches.

Quantum mechanics concerns the physics of tiny particles, like electrons or photons. Unlike macroscopic objects, these particles behave very differently. For instance, their position and momentum cannot be determined explicitly, but only in terms of a given probability. This is called the Heisenberg uncertainty principle. The state of a particle is represented by a function |ψ⟩, which can be used to determine the probability that a particle can be found in a specific region. The evolution of |ψ⟩ in time is given by the Schrödinger equation.

A variation of this equation is the Wigner equation. In contrast to the Schrödinger equation, the Wigner equation is not a differential equation, but it is an integral equation. The function we are looking for is the Wigner function f_w. It is a quasi-distribution function which depends on the position x and the momentum p and can be used to determine the mean value of a physical quantity of a particle, such as its total energy.

The goal of this project is to find an algorithm which can simulate the evolution of the Wigner function f_w in a linear electromagnetic field. First, the Wigner equation for this case was derived. The derivatives were then approximated using finite difference schemes. In order to simplify the equation, the position x and momentum p were then replaced by functions x(t) and p(t), respectively. These functions represent the trajectory of a classical charged particle in an electromagnetic field. Then, the Wigner equation was transformed into a Fredholm integral equation. The general solution of these types of equations is the Liouville-Neumann series. Each element of this series contains an integral which must be approximated.

A common means to approximate definite integrals is the Monte Carlo method. The integrals can be evaluated either forward or backward in time. The initial state is given by a function f₀. For each iteration, a particle is generated at a random point (p,x). The particle then follows the trajectory until the final time is reached. Using the time-discretized finite difference method, the particle is scattered several times. This means that, at a certain point in time, factors ΔP and ΔX are added to the current momentum p(t) and position x(t), respectively. The particle subsequently continues to follow its trajectory. Upon reaching its final location, the desired physical quantity of the particle is evaluated at this point. By repeating this process several times and calculating the stochastic average, one can approximate the mean value of a physical quantity of the simulated particle.

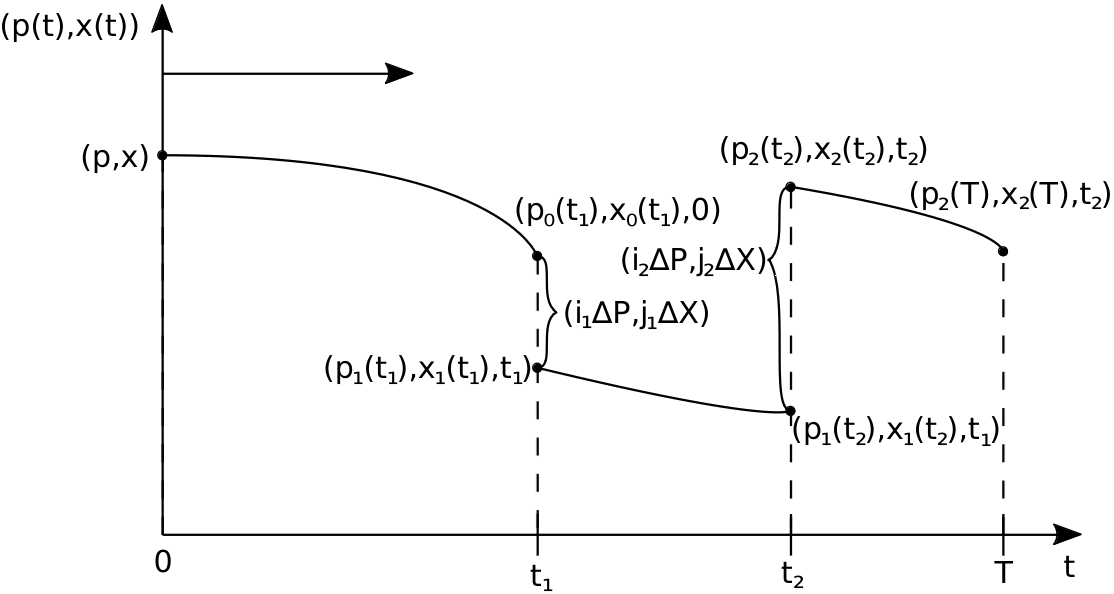
Fig. 1: The trajectory of p(t) and x(t) is projected onto the y-Axis. The particle starts at (p,x,t=0) and moves forward in time in phase space according to the Lorentz force F. When the particle reaches t₁ it is scattered, i.e., a factor (ΔP,ΔX) is added. Afterwards, it follows the trajectory again until it reaches t₂. This process is repeated until t=T is reached, when the physical quantity A_T is evaluated.