 |
|
||||
BiographyJosef Gull was born in Vienna in 1996. In 2022, he completed the Master's Programme Microelectronics and Photonics at TU Wien. He is currently working towards his doctoral degree as a project assistant on the development of Monte Carlo methods for the solution many-body kinetic equations. |
|||||
Electron-Electron Scattering in Semiconductors
For the simulation of high-energy electrons, the inclusion of electron-electron interactions due to Coulomb forces is essential. However, most transport models allow only an approximate treatment of this effect because they are based on a single particle formalism. Our goal is to develop a Monte Carlo algorithm which includes the effects of electron-electron scattering (EES) in semiconductors in an efficient way. The challenge in developing such an algorithm is that the Boltzmann transport equation becomes nonlinear, when considering this scattering mechanism. Earlier attempts, therefore, were based on self-consistent iterative approaches or on other severe approximations. In our algorithm, we simulate the trajectories of two electrons simultaneously. Both electrons experience phonon-scattering and EES. Algorithms for stationary and transient bulk simulations, as well as stationary device simulations, have been developed. We have observed that in bulk simulations, EES did not affect the velocity-field curve and the mean energy as a function of the electric field. Also, the energy and momentum distributions are not altered by EES.
We used an ensemble Monte Carlo algorithm for the transient simulations. An ensemble of trajectory pairs is sampled at equidistant time steps. An example is the mixing of hot carriers and carriers in equilibrium with the lattice, a situation typically occurring in the drain region of a field-effect transistor (FET). Maxwellian distributions determine the initial momentum for the hot electrons (3,000 K) and electrons at equilibrium (300 K). Due to EES, the energy of the hot carriers relaxes much faster than it does if only phonon scattering is present (see Fig. 1).
The proposed algorithm has been extended to account for one-dimensional potential profiles. For a simplified description, we call one electron the sample electron (SE) and the second electron the partner electron (PE). The simulation domain consists of cells, each holding one PE. In the algorithm, we inject an SE at the cell boundary and simultaneously calculate the free flight trajectories of the SE and PE. Let us suppose that one of the two electrons leaves the cell before a scattering event takes place. In this case, we sample the state at the cell boundary and calculate a new pair of trajectories, according to the electric field of the next cell. If the PE leaves the cell before the SE, the electrons swap their PE and SE roles. The swap ensures that every cell always holds one PE, and that the algorithm treats both electrons equally. A simulation of the energy distribution in the channel region of a FET is provided in Fig. 2. We found that including EES alters the thermal tail, typically observed in simulations with phonon-scattering only.
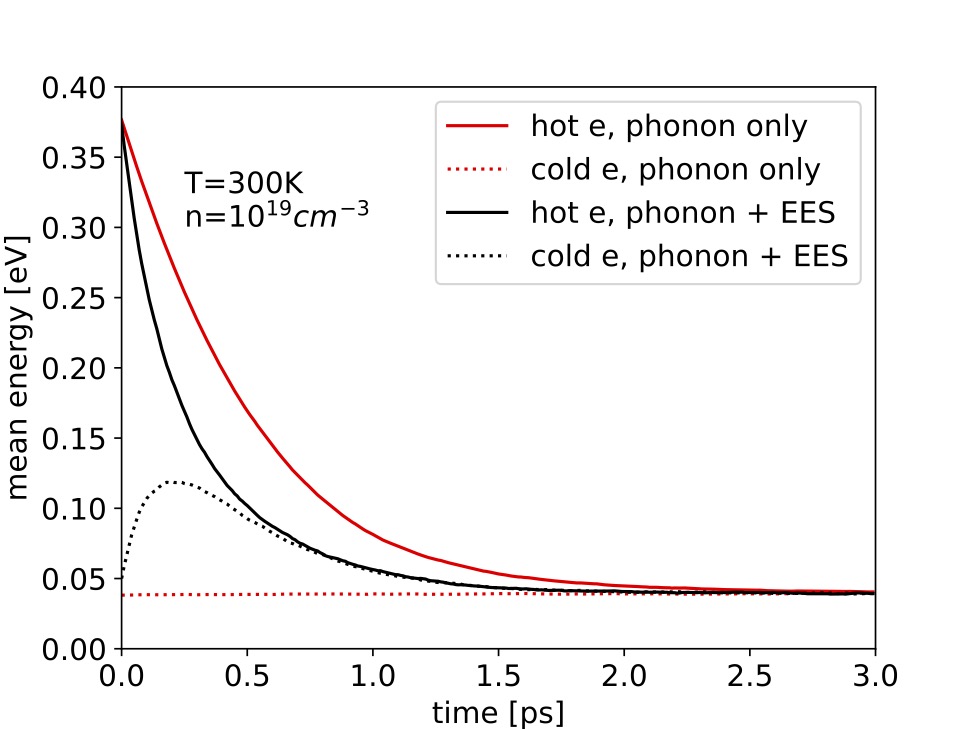
Fig. 1: Mixing of hot and cold carriers in bulk. Initial temperatures are T0=300 K (cold electron) and T0=3,000 K (hot electron).
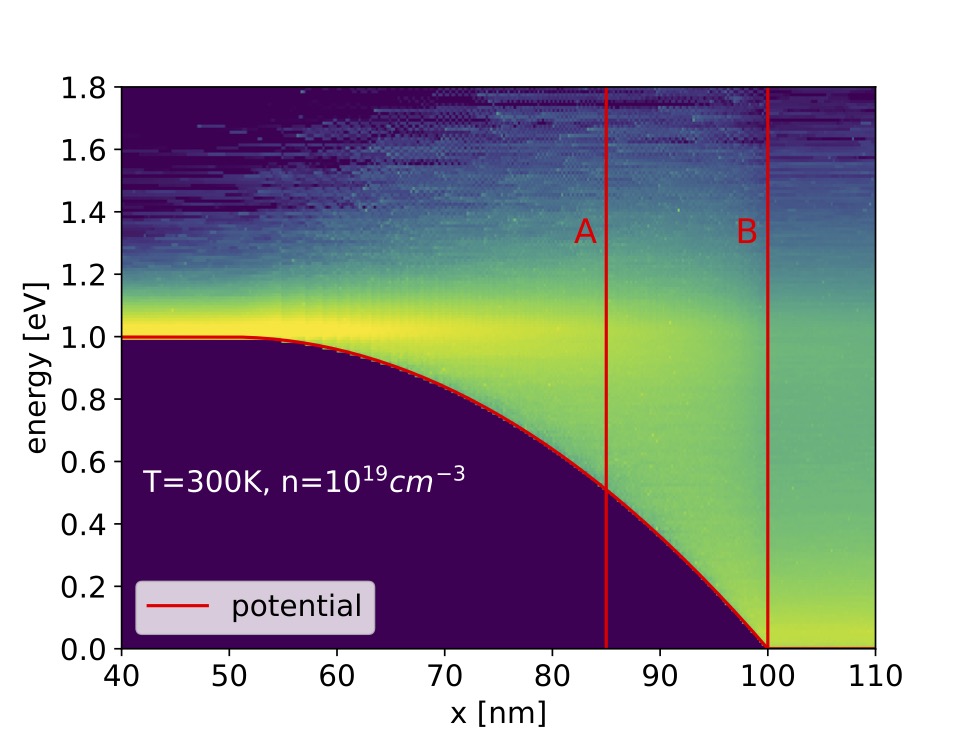
Fig. 2: Energy distribution in a channel potential. A and B note the positions at which the potential dropped by 0.5 eV and 1 eV, respectively.


