 |
|
||||
BiographyClemens Etl was born in Wr. Neustadt, Austria, in 1990. He studied Technical Mathematics at the TU Wien where he received his master's degree in 2019. After graduation, he worked as a scientific assistant in the field of artificial intelligence at the Know-Center in Graz. He joined the Institute for Microelectronics in May 2022 where he is currently working on his doctoral degree. He is researching high performance electron quantum transport modeling and simulation approaches. |
|||||
Gauge-invariant Wigner Theory
The investigation of single-electron dynamics is relevant for fields like quantum optics, nanoelectronics, and quantum computing. One way to describe the quantum mechanical evolution of an electron is the Wigner formalism, where the state of an electron is given by the Wigner function, which depends on the electron's location and canonical momentum. However, this formulation depends on the choice of the electrodynamic potentials A and φ, which are not unique for a given electromagnetic field. This leads to an ambiguity in the definition of the Wigner function that can significantly complicate the interpretation of physical phenomena.
A gauge-invariant reformulation of the Wigner function was done in 1956 by Stratonovich. The so-called Stratonovich function, which depends on the kinetic momentum instead of the canonical momentum, has not been analyzed in depth yet. Therefore, we investigated the physical properties of this function. Most of the properties, such as real-valuedness, time and space symmetry, and boundedness, are inherited from the Wigner function. However, there is one major difference between the two formulations: While the probability distribution of the electron's canonical momentum can be expressed through the Wigner function, the probability distribution of the kinetic momentum cannot be expressed through the Stratonovich function due to Heisenberg's uncertainty principle.
We have also derived an evolution equation for the Stratonovich function, representing a gauge-invariant Wigner equation, which can be expressed as a local pseudo-differential equation or a non-local integral equation. These formulations are also well suited to derive semiclassical approximations up to arbitrary order in the Planck constant. In the figure below one can see that these terms lead to a redistribution of the electron's density, while the trajectory of the center of mass remains the same, in accordance with the Ehrenfest theorem.
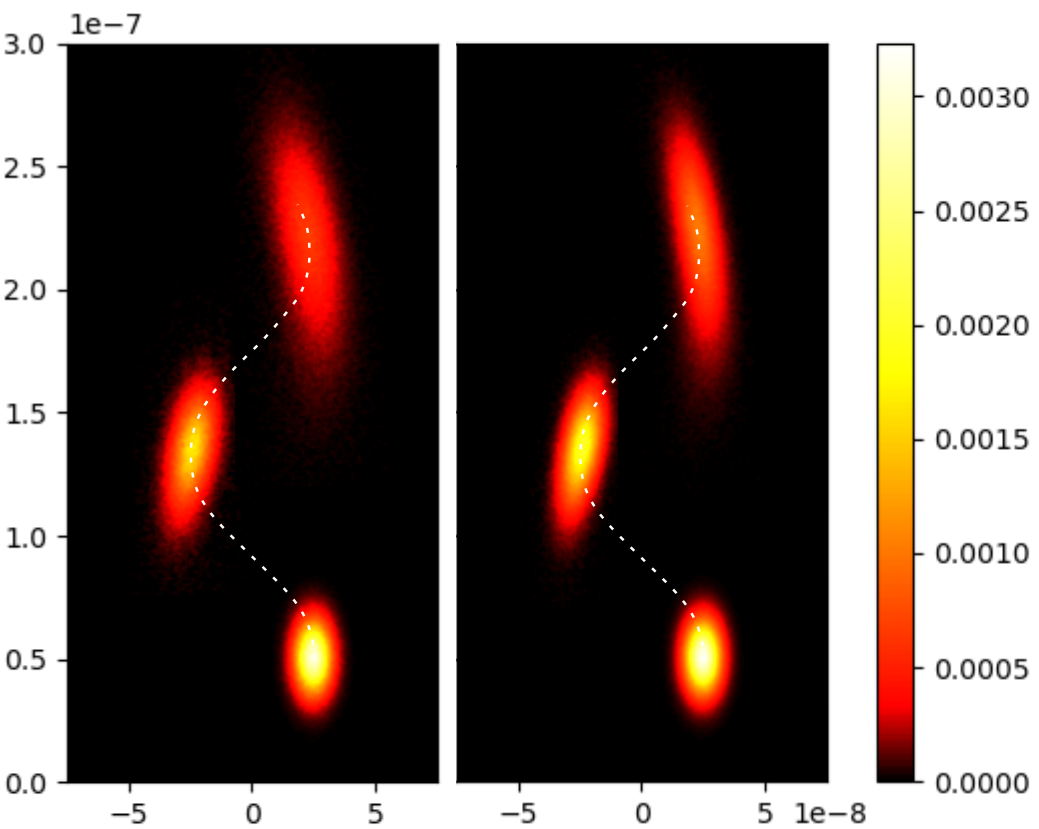
Fig. 1: Evolution of an electron in a linear magnetic field: Quantum evolution (left) vs. classical evolution (right)


