 |
|
||||
BiographyJosef Gull was born in Vienna in 1996. In 2022, he completed the Master's Programme Microelectronics and Photonics at TU Wien. He is currently working towards his doctoral degree as a project assistant on the development of Monte Carlo methods for the solution many-body kinetic equations. |
|||||
Simulation of Energy Distribution via Two-Particle Monte Carlo Transport
We are developing an electronic transport model aimed at revealing the energy distribution within electronic devices — a crucial aspect for understanding degradation mechanisms such as hot carrier degradation (HCD) in MOSFETs. Traditional Monte Carlo simulations in silicon often rely on the parabolic band approximation for the conduction band, which limits accuracy at higher kinetic energies — particularly in nanoscale devices with steep potential gradients. To address this, we have already implemented an electron-electron scattering (EES) model within the Kane dispersion framework. This year, we extended our efforts by formulating the corresponding kinetic equation in two dimensions. Additionally, we addressed the reduced accuracy at higher energies—where carrier occupancy is low—by developing a dedicated statistical enhancement algorithm.
Since the current code samples the electron state at the boundaries of simulation cells, an algorithm is required to accurately determine the time at which an electron exits a cell. This requires solving the equations for the electron’s x(t) and y(t) positions simultaneously. The solution is computed numerically using a Newton scheme, with a Brent method employed as a fallback.
Figure 1 illustrates the impact of using different dispersion models. While the trajectories under the parabolic (blue) and Kane (red) models appear visually similar, their lengths differ significantly. Using the parabolic model’s exit time based on an energy-dependent effective mass m=m0(1+αE(t0)) can underestimate the exit time for the Kane trajectory—sometimes leading to significant errors, as highlighted by the prominent red cross in Figure 1 (right).
Steady-state problems are inherently time-invariant, allowing the repeated simulation of N time frames, all starting from a high-energy device state, with each frame weighted by 1/N. A cascaded implementation of the statistical enhancement algorithm yielded promising results.
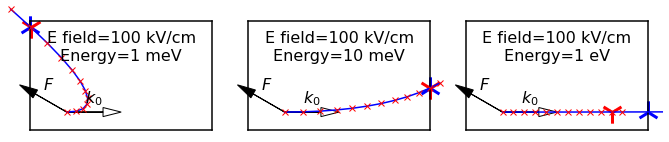
Fig. 1: Comparison of trajectories in Kane (red) and parabolic (blue) dispersion for different initial energies. The thick cross marks the position at the exit time calculated from the parabolic model.


