 |
|
||||
BiographyJohann Cervenka was born in Schwarzach, Austria, in 1968. He studied electrical engineering at the Technische Universität Wien, where he received the degree of Diplomingenieur in 1999. He then joined the Institute for Microelectronics at the Technische Universität Wien and received his PhD in 2004. His scientific interests include three-dimensional mesh generation, as well as algorithms and data structures in computational geometry. |
|||||
Extension of the Deterministic Approach of the Wigner Formalism to Two Dimensions
Developing novel nanoelectronic devices requires simulation methods capable of accurately modeling quantum mechanical effects in carrier transport processes. The Wigner formalism provides a convenient framework by representing quantum mechanics in phase space, making it particularly well-suited for such simulations.
The developed approach adopts an integral formulation of the Wigner equation, by avoiding direct discretization of the rapidly varying terms. In the transition from one-dimensional to two-dimensional (2D) systems, new challenges emerge, where computational complexity and stability issues become more pronounced.
The method currently under examination tracks the evolution of the entire distribution function in phase space using a Lawson-type predictor-corrector scheme.
This scheme consists of two main stages to estimate the system’s future state based on the current distribution:
- Prediction: An explicit step estimates the next state of the distribution based on the current state.
- Correction: This estimate is iteratively refined to improve accuracy for the next time step.
Preliminary results demonstrate the distribution function of a propagating 2D Gaussian wave packet approaching a rectangular potential barrier. In the figure the situation of a wave packet moving rightwards after reflection of the center part of the package is shown, while distant regions passed-by the barrier. Notably, while previous simulations required parallel computing on multiple nodes, the new approach achieves comparable results on a single compute node, marking a significant improvement in efficiency and scalability for 2D quantum transport simulations.
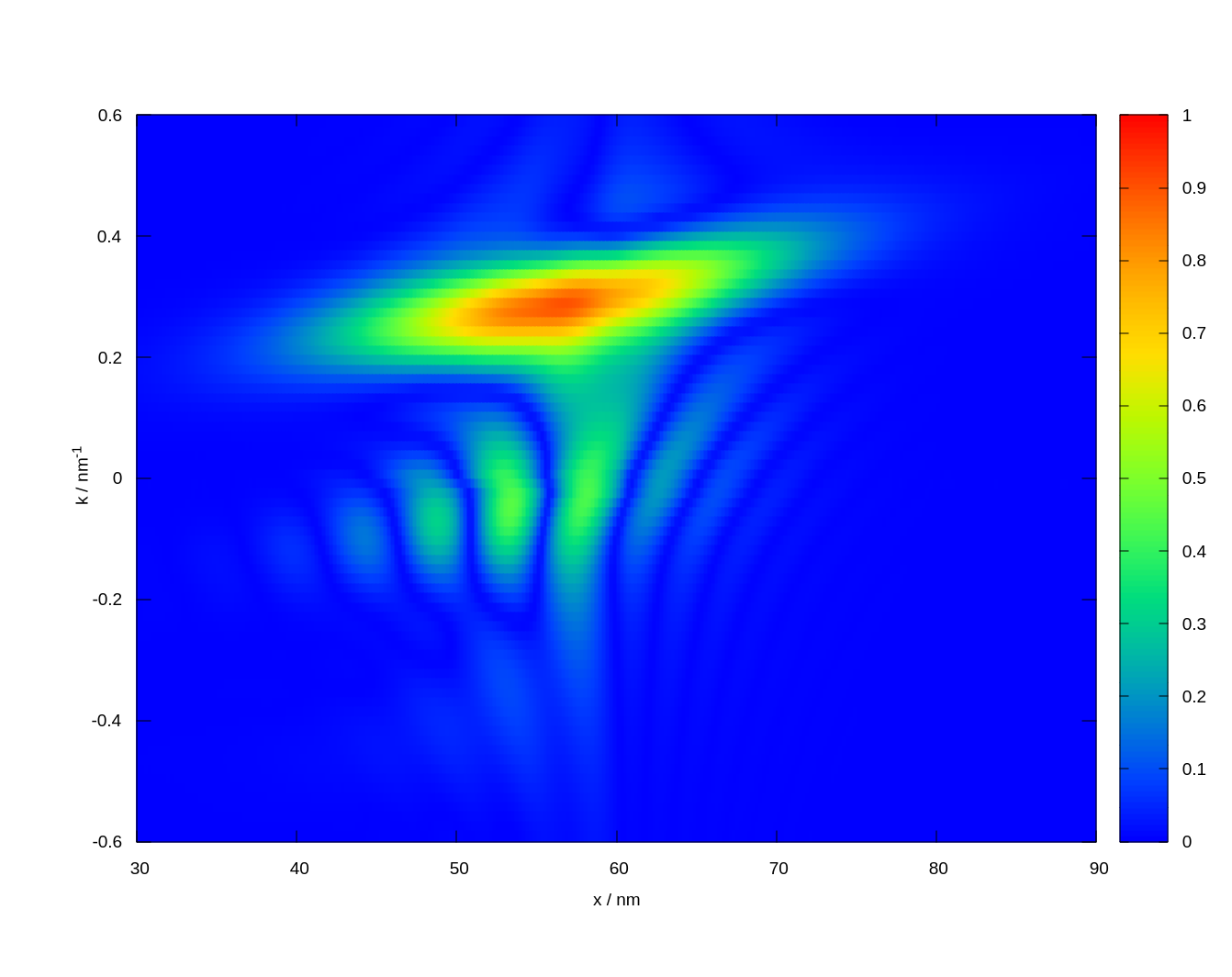
Fig. 1: Propagation of a Gaussian wave packet reaching a potential barrier in two dimensions


