2.2 Rayleigh-Ritz Method

The Rayleigh-Ritz method seeks a stationary point of a variational functional. For operators 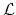$\mathcal{L}$ which are self-adjoint and positive-definite, the stationary point of the functional,

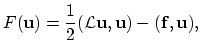$$F(\mathbf{u})=\frac{1}{2}(\mathcal{L}\mathbf{u},\mathbf{u})-(\mathbf{f},\mathbf{u}),$$ (2.4)

is an exact solution of (2.1), assuming 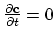$\frac{\partial \mathbf{c} }{\partial t}=0$. In (2.4) the inner product of the two vector functions is defined as,

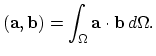$$(\mathbf{a},\mathbf{b})=\int_{\Omega}\mathbf{a}\cdot\mathbf{b} d\Omega.$$ (2.5)

The functional 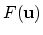$F(\mathbf{u})$ reaches a minimum for the function 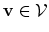$\mathbf{v}\in \mathcal{V}$, if the first variation 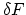$\delta F$ is zero for this function, or equivalently,

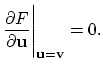$$\frac{\partial F}{\partial \mathbf{u}}\Bigg\vert_{\mathbf{u}=\mathbf{v}}=0.$$ (2.6)