A time step and mesh should always be chosen in a such a way that the error made during the numerical solving procedure is acceptably small. In this chapter we consider a general system of nonlinear PDEs and there is no rigorous theory available which covers the error behavior of such systems. However for certain special classes of problems there are well-known results which can be used as basis for the study of more complex systems.
For our purpose the case
![]() and
and
![]() in (2.1) is of special interest, since it represents the problems discussed in this work in its simplest form.
in (2.1) is of special interest, since it represents the problems discussed in this work in its simplest form.
Using a backward Euler scheme and a finite element method with linear basic nodal functions we have the estimate [13,10,9],
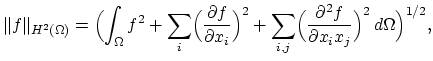 |
(2.52) |
Taking into account that the logarithmic quantity in (
![]() ) changes slowly, it can be absorbed in the constant
) changes slowly, it can be absorbed in the constant ![]() and considering that,
and considering that,
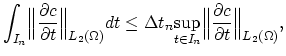 |
(2.53) |
The first term on the right side of (2.54) corresponds to the time discretization error and the second to the spatial discretization error [13].
If we want to achieve the time discretization error to be bounded by ![]() for
for ![]() , we have to ensure that,
, we have to ensure that,
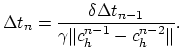 |
(2.57) |
To estimate the error of the spatial finite element discretization several methods are known today. These methods are based on the estimation of the second term on the right side of (2.54) using the solution obtained by means of the finite element method (a posteriori error estimators)[13,10,9].
First we will present the flux error estimator based on the work by Babuska, Bieterman, and Rheinboldt [9].
We consider a tethraedron
![]() and define a tehraedron-patch
and define a tehraedron-patch ![]() as the subset of
as the subset of
![]() of all tethraedrons which have one common face with
of all tethraedrons which have one common face with ![]() .
Each point
.
Each point ![]() of the discretization holds a concentration value
of the discretization holds a concentration value ![]() and inside of the each element the concentration is linearly interpolated as
and inside of the each element the concentration is linearly interpolated as
![]() . In the following we omit the discrete time index
. In the following we omit the discrete time index ![]() , because we consider only a single time step.
, because we consider only a single time step.
The concentration gradient, calculated by
![]() , is constant on each element
, is constant on each element ![]() and discontinuously changes between two neighboring elements. We write
and discontinuously changes between two neighboring elements. We write
![]() for
for
![]() .
This discontinuity expresses the error of the approximation and can be quantified on the tehraedron-patch
.
This discontinuity expresses the error of the approximation and can be quantified on the tehraedron-patch ![]() as the flux error estimator,
as the flux error estimator,
![$\displaystyle e_{F}^2(T_0)= h^2\sum_{T\in P(T_0)}\int_{T\cap T_0}\Bigl[\frac{\partial C}{\partial\mathbf{n}} \Bigr]^2_{T,T_0} df,$](img227.png) |
(2.58) |
![$\displaystyle \Bigl[\frac{\partial C}{\partial\mathbf{n}} \Bigr]_{T,T_0}=\mathbf{n}\cdot(\nabla_T C - \nabla_{T_0} C),$](img228.png) |
(2.59) |
The second spatial discretization error estimator presented here is the gradient recovery error estimator which is widely used today in the finite element community [14].
For the derivation of the gradient recovery error estimator we first need the recovered gradient.
The recovered gradient is calculated as the Lagrange interpolate at the nodes of the mesh.
Taking a node
![]() and defining
and defining ![]() as a point-patch of all elements which contain node
as a point-patch of all elements which contain node ![]() as one of its nodes.
The recovered gradient
as one of its nodes.
The recovered gradient
![]() at the node
at the node ![]() , is then calculated as,
, is then calculated as,
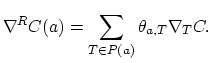 |
(2.60) |
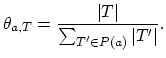 |
(2.61) |
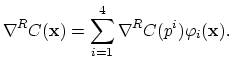 |
(2.62) |
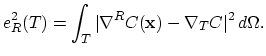 |
(2.63) |
For the applications discussed in this thesis the physically motivated dosis error estimator (Section 3.9) has even more importance than the error estimators presented above.
Independent of the actual mesh adaptation strategy and error estimator, the following algorithm for the finite element adaptive computation can be applied [15],

Here ![]() denotes the total error,
denotes the total error, ![]() is an error estimator,
is an error estimator,
![]() or
or
![]() , and
, and ![]() is a given tolerance for the relative error.
is a given tolerance for the relative error.