B. Some Tools from Abstract Mathematical Analysis

Let V be a Hilbert space and $(\cdot,\cdot)_V$ and $\Vert\cdot\Vert _V$, the corresponding scalar product and norm, respectively. A linear form (or linear functional) $L$ on $V$ is a function $L:V\rightarrow\Bbb{R}$ such that,

$$L(\lambda u+\mu v)=\lambda L(u)+\mu L(v),\quad \forall u,v\in V, \lambda,\mu\in\Bbb{R}.$$ (B.1)

A linear form $L$ is bounded if there is a constant $\Lambda\in\Bbb{R}^+$ such that,

$$\vert L(u)\vert\leq \Lambda \Vert u\Vert _V,\quad \forall u\in V.$$ (B.2)

A bilinear form on $V$ is a function $a:V\times V\rightarrow\Bbb{R}$, which is linear in each argument separately, i.e., such that, for all $u,v,w\in V$ and $\lambda,\mu\in\Bbb{R}$,

$$a(\lambda u+ \mu v,w)=\lambda a(u,w)+\mu a(v,w),$$ (B.3)

$$a(w,\lambda u+ \mu v)=\lambda a(w,u)+\mu a(w,v).$$ (B.4)

The bilinear form $a(\cdot,\cdot)$ is said to be symmetric if,

$$a(u,v)=a(u,v),\quad \forall u,v\in V,$$ (B.5)

bounded if there is a constant $\gamma\in\Bbb{R}^+$ such that,

$$\vert a(u,v)\vert\leq \gamma \Vert u\Vert _V \Vert v\Vert _V,\quad \forall u,v\in V,$$ (B.6)

and $V-elliptic$ if there is a constant $\alpha\in\Bbb{R}^+$ such that,

$$\vert a(u,u)\vert\geq \alpha \Vert u\Vert _V^2.$$ (B.7)

The set of all bounded linear functionals on $V$ is called dual space of $V$ and denoted $V^*$. The norm in $V^*$ is given by,

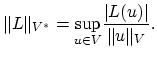$$\Vert L\Vert _{V^*}=\underset{u\in V}{\text{sup}}\frac{\vert L(u)\vert}{\Vert u\Vert _V}.$$ (B.8)

Theorem I (Riesz's representation theorem): Let $V$ be a Hilbert space with scalar product $(\cdot,\cdot)$. For each bounded linear functional $L$ on $V$ there is an unique $u \in V$ such that,

$$L(v)=(v,u),\quad \forall v\in V.$$ (B.9)

Moreover,

$$\Vert L\Vert _{V^*}=\Vert u\Vert _V.$$ (B.10)

Theorem II (Lax-Milgram lemma): If the bilinear form $a(\cdot,\cdot)$ is bounded and $V$-elliptic in the Hilbert space $V$, and $L$ is bounded linear form in $V$, than there exists a unique vector $u \in V$ such that,

$$a(u,v)=L(v),\quad\forall v\in V,$$ (B.11)

and,

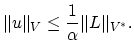$$\Vert u\Vert _V\leq \frac{1}{\alpha}\Vert L\Vert _{V^*}.$$ (B.12)

Theorem III: Assume that $a(\cdot,\cdot)$ is a symmetric, $V$-elliptic bilinear form and that $L$ is a bounded linear form on the Hilbert space $V$. Than $u \in V$ satisfies (B.11) if and only if,

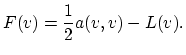$$F(u)\leq F(v),\quad \forall v \in V, F(v)=\frac{1}{2}a(v,v)-L(v).$$ (B.13)