


Next: 4.2 Prerequisites for Applying
Up: 4. An Alternative Approach
Previous: 4. An Alternative Approach
The simple linear diffusion differential equation reads
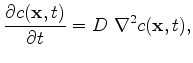 |
(4.1) |
where 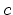 denotes the time and space dependent concentration,
with a constant diffusion coefficient
denotes the time and space dependent concentration,
with a constant diffusion coefficient 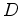 and the initial condition
and the initial condition
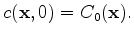 |
(4.2) |
With the theory of Green's Functions the solution
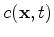 of this differential equation problem for one, two, and three dimensions is obtained as
of this differential equation problem for one, two, and three dimensions is obtained as
where
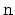 is the dimensionality of the problem.
is the dimensionality of the problem.
The discretization of this problem is performed by the following method:
After the simulation domain is meshed and the Delaunay boxes are determined, the initial distribution
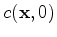 is discretized on the grid points by Dirac functions
is discretized on the grid points by Dirac functions
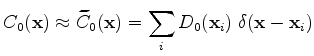 |
(4.4) |
with
The preservation of the total implantation dose in the simulation domain
is guaranteed by the discretization of the initial distribution.
As a consequence by applying (4.3), the approximated transient concentration distribution can be evaluated by
The total dose in the whole space
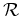
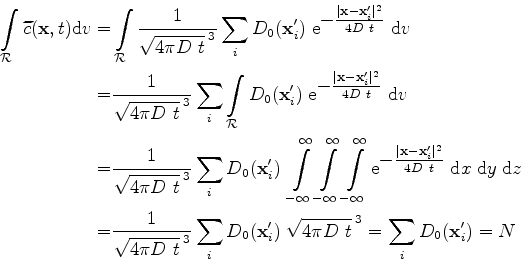 |
(4.8) |
is preserved, too. The preservation of the implanted dose is a significant and necessary condition for the quality of the method. In total, the amount of implanted ions must not change during the diffusion process. Therefore, the discrete formulation must fulfill this preservation, too.
Since the implantation distribution is delivered on a grid, this grid can be used for calculating the entire dopant diffusion process. In this case, the initial dopant concentration
 is defined on the grid points
is defined on the grid points  and therefore, the integration of (4.5) can be omitted and replaced by
and therefore, the integration of (4.5) can be omitted and replaced by
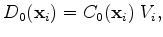 |
(4.9) |
which is the initial concentration at the grid point, weighted by the control volume of the Voronoi box.



Next: 4.2 Prerequisites for Applying
Up: 4. An Alternative Approach
Previous: 4. An Alternative Approach
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation
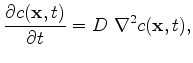
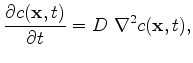
![]() is discretized on the grid points by Dirac functions
is discretized on the grid points by Dirac functions
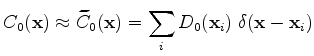
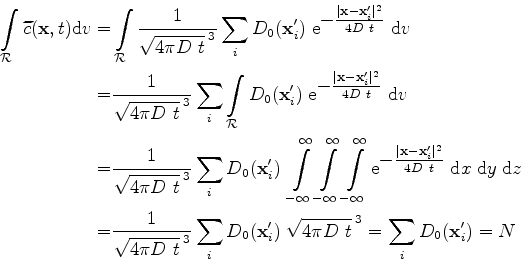
![]() is defined on the grid points
is defined on the grid points ![]() and therefore, the integration of (4.5) can be omitted and replaced by
and therefore, the integration of (4.5) can be omitted and replaced by