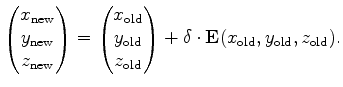 |
(5.64) |
When applying the potential method, not all of the device segments can be used as such capacitors. Because of the strong nonlinearities of the coupled differential equations (refer Section 5.1), the grid resolution on the semiconductor segment must be high. While this method works well on the semiconductor segment of a device, on other segments it may be impossible to define the six sides of the cuboid. Sometimes an automatic search for the sides will not be possible and, due to the complexity of user interaction on three-dimensional data, this way would not seem feasible anyway.
An alternative variant of this method can be derived by only selecting two opposite electrodes of the capacitor. These electrodes can be selected in a more general way, for example by selecting interface boundaries between different segments. The equipotential surfaces are evaluated similarly, but different to the previously described method, the surface of these electrodes is triangulated and the intersections of equipotential surfaces and field lines starting from the boundary points are delivered to the grid generator. The field lines have to be evaluated directly, not indirectly via the dual electric fields, but by walking along the directions of the electric field.
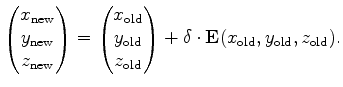 |
(5.64) |
Unfortunately these methods have a fundamental disadvantage. If a grid point is inserted at the electrode surface (maybe a geometry point), it will cause many grid points at the intersections with the equipotential planes. Moreover, inserting an additional potential tick causes a lot of grid points along the field lines. For preventing this induced point insertion, the use of point deletion algorithms similar to a terminating lines algorithm for ortho grids is necessary.
The previously described methods disperse grid points by a selected method and the grid generation is done by a Delaunay grid generator. The satisfaction of the Delaunay criterion is necessary for the following device simulation that is based on Finite Boxes. Other methods of directly splitting edges of an initial grid are also feasible. To prevent obtuse angles in the tetrahedrons, usually the longest edges of the tetrahedrons are split. Especially with a combination with the potential method, the lengths of the edges can be weighted directionally dependent on size and direction of the electric field. Using this method also an anisotropic grid can be obtained. However, as the grid lines are split directly to obtain the desired grid density and no afterwards Delaunay tetrahedrization is performed, the satisfaction of the Delaunay criterion cannot be guaranteed by this method and it cannot be used for Box Integration. Applications for oxidation simulation using Finite Elements had still been performed by this method [73].