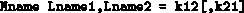
Eine ideale Kopplung zwischen zwei Induktivitäten wird mit folgender Anweisung beschrieben:
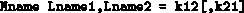
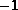bis 
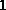liegen.
Wird nur ein k12 angegeben, liegt eine symmetrische Kopplung vor.
Bei einer asymmetrischen Kopplung gibt der erste Wert die Kopplung von
Lname1 zu Lname2, der zweite die Kopplung von
Lname2 zu Lname1 an.
Die beiden Induktivitäten Lname1 und Lname2 werden als gleichsinnig gewickelt betrachtet, wenn der Kopplungsfaktor positiv ist.
Die charakteristischen Gleichungen der Kopplung sind als
additive Terme in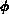 
des Flusses 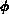der beiden betroffenen
Induktivitäten definiert.
Die Teile der Gleichung, die nicht durch die Kopplung entstehen,
sind in den folgenden charakteristischen Gleichungen durch 
gekennzeichnet.
Die Induktivitätsmatrix, eine Matrix mit den beteiligten Induktivitäten in der Hauptdiagonale und den Gegeninduktivitäten in den entsprechenden Nebendiagonalen, muß positiv definit sein, d.h. alle Eigenwerte der Matrix müssen größer als 0 sein. Ist diese Bedingung nicht erfüllt, ist die Lösung des Netzwerkes nicht stabil, d.h. das Ergebnis wächst über alle Grenzen.