



Next: 2.3 State of the
Up: 2. Challenge and Demands
Previous: 2.1 CAD
The demands can be roughly categorized.
- automatic mesh generation of complex semiconductor devices
within an integrated framework of simulators
- anisotropic geometrical requirements (structure dependent)
- mesh density grading, anisotropic density requirements
(application dependent)
- finite element mesh quality and closed control volumes for
finite volume methods
Combined full scale three-dimensional process and device simulation has
suffered from the lack of available TCAD tools for the various established
data formats in the field. A framework of such a TCAD environment
providing the necessary tools is itself still a subject to research
and development [79,172,182]. Aside from preliminary means to couple and control some of the
simulators [173,121,185], powerful geometry processors are missing.
Considerable person power is consumed to detect inconsistencies in a
tedious manner, and to debug structures that the mesher should, but
does not mesh.
Such structures typical for semiconductor simulation purposes often
exhibit extreme ratios between the size of the smallest and the largest
features, where no structural simplifications can be afforded. Only
quantitative data reduction may be performed to decrease the amount of
redundant data.
Once the mesher is provided with a valid and clean model it has to
deal with the topographical as well as topological complexity of the
underlying geometry which contains many internal surfaces, edges
sharing more than two facets, and thin layers.
- Thin Layer
- Two polygonal surfaces with a large area compared to
the maximal local feature size
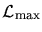 measured inbetween.
Less general subtypes are formed when the surfaces are
planes. Furthermore, the planes might be parallel or have normals in
the direction of a coordinate axis. For the simplest case of two
parallel planes their normal distance
measured inbetween.
Less general subtypes are formed when the surfaces are
planes. Furthermore, the planes might be parallel or have normals in
the direction of a coordinate axis. For the simplest case of two
parallel planes their normal distance
![$d = \alpha \mathcal{L},
\alpha \in [1..2]$](img29.gif) is small compared to their lateral expansion
(Fig. 2.2).
is small compared to their lateral expansion
(Fig. 2.2).
It is relevant especially in three dimensions to detect such precisely
defined thin layers in order to avoid an unnecessary high number of
mesh elements. While standard isotropic
elements are still manageable in two dimensions, the number of
isotropic elements in three dimensions roughly increases quadratically
with the ratio of lateral edge length to
 .
It will be necessary independent of the physical application or
solution quantity and due to a pure geometrical feasibility that the mesh
generator enforces anisotropic elements at automatically detected
regions which convey anisotropic geometrical information.
The most general and sophisticated algorithms
have to be applied in order for the mesh generator to deal with
automatically generated structures.
Computer generated topographies not only evolve
from etching and depositon modules, but also through three-dimensional
extraction of geometrical data from two-dimensional simulations and
through solid modelers deriving their information from layout data.
An automatic geometry preprocessor and mesh generator can complete
the integrated framework system and enable the fast and efficient
optimization of various design and manufacturing parameters.
.
It will be necessary independent of the physical application or
solution quantity and due to a pure geometrical feasibility that the mesh
generator enforces anisotropic elements at automatically detected
regions which convey anisotropic geometrical information.
The most general and sophisticated algorithms
have to be applied in order for the mesh generator to deal with
automatically generated structures.
Computer generated topographies not only evolve
from etching and depositon modules, but also through three-dimensional
extraction of geometrical data from two-dimensional simulations and
through solid modelers deriving their information from layout data.
An automatic geometry preprocessor and mesh generator can complete
the integrated framework system and enable the fast and efficient
optimization of various design and manufacturing parameters.
The range of the simulated magnitude (e.g. the concentration during
diffusion simulation or in device simulation) covers several exponents
and leads to difficulties when discretized with conventional meshes.
The variation of the local mesh density over space and over direction
(anisotropic mesh density) is the key factor to keep the size of the
mesh manageable and at the same time the discrete distribution of the
magnitude accurate.
A balance between the number, the size, and the quality of the
elements must be achieved for such a good mesh grading.
The number should be minimized while the size should satisfy local
density criteria. Often, the mesh is not optimally fitted and too
coarse or too fine elements exist in various areas of the simulation
domain. Alternatively, the desired accuracy of the analysis cannot be
achieved in all areas, or the subsequent tools and simulators are
pushed to limits beyond the scope of an average computer by a
generally too fine mesh. An increased flexibility in refinement
allowing for rapid changes of the mesh density while
keeping the overall element count low would be ideal. This flexibility
cannot be increased infinitely. The rapid change of element size is
limited under the premise of maintaining a certain element quality.
The finite element method requires that the elements possess a certain
geometrical quality. It can have a very bad influence on the convergence of
the solution if the elements have extremely obtuse angles.
The angle spanned by two planes (dihedral angle) becomes an important
measure in three dimensions (Chapter 3). Achieving good
bounds on the dihedral angle of the elements becomes a major demand in
three-dimensional finite element mesh generation.
The finite volume or control volume method which is often also called
the box integration method is crucial for semiconductor device simulation,
because it can be combined with the Scharfetter-Gummel scheme
[58][119][146] which takes the exponential carrier
concentration into account.
As will be discussed in Chapter 3 ``closed'' control
volumes are required which is usually accomplished by constructing a
Voronoi [117] type mesh. The Voronoi box
associated with each point from the mesh satisfies the requirements
and possesses some advantages as opposed to e.g. boxes which are
defined by centroids (gravity boxes).
The common approach to obtain such a Voronoi tessellation is to
construct its dual Delaunay Triangulation. (See
Chapter 5 for a description of the Delaunay theory
and its definitions.)
Stable Delaunay meshing of a complex semiconductor structure is a
demanding effort in three dimensions.
The generalization of a two-dimensional to a three-dimensional
Delaunay Triangulation poses not a mere quantitative but rather a
qualitativ challenge (Chapter 5).
Among other reasons is that a bounded dihedral angle between facets of
the input structure becomes a crucial factor for a provably
terminating Delaunay algorithm. With an increasing number 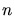 of points in three dimensions, keeping the
computational complexity below O(
of points in three dimensions, keeping the
computational complexity below O(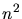 ) is another crucial
requirement for success.
) is another crucial
requirement for success.
The tasks can be summarized in relation to their application.
- Meshing of comparatively simple (near
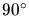 dihedral angles
between input facets) but huge structures composed of a large number
of vias and lines. Simulation of 3D Interconnects.
dihedral angles
between input facets) but huge structures composed of a large number
of vias and lines. Simulation of 3D Interconnects.
- Handling the minimum and possibly faulty information on arbitrary
complex structures provided by topography simulation
with eventually moving structure boundaries [45].
Semiconductor process simulation.
- Resolving highly non-linear quantities with a directional mesh
density which is not only limited to the three directions of the
cartesian axises (physical anisotropy).
Semiconductor device simulation.
- Dealing with strongly acute dihedral angles between input facets
and extreme ratios between local edge lengths and local feature size
(geometrical anisotropy).
Semiconductor process and device simulation.




Next: 2.3 State of the
Up: 2. Challenge and Demands
Previous: 2.1 CAD
Peter Fleischmann
2000-01-20
![]() of points in three dimensions, keeping the
computational complexity below O(
of points in three dimensions, keeping the
computational complexity below O(![]() ) is another crucial
requirement for success.
) is another crucial
requirement for success.