5.2.3 Results

This example has shown that with SIESTA it is indeed possible to determine the thermal coefficients of the electrical and thermal conductivities of polysilicon and polycide only from electrical measurements. This offers the possibility to minimize the computational as well as monetary effort for timely expensive caloric measurements.

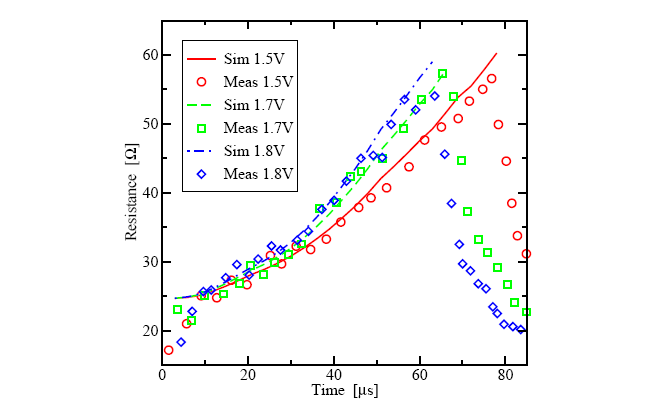
With additional consistency checks within the simulator and the optimization framework, intermediate simulation results can be verified whether the obtained data is physically reasonable. The process of the parameter identification took therefore a certain time longer than expected, but has yielded excellent agreement with measurements as shown in Figure 5.14, Figure 5.15, and Tab. 5.1. Identified material parameters are summarized in Tab. 5.1, where the extracted coefficients are compared to data found in the literature [137,343,344]. The wide range of certain parameters shown in Tab. 5.1 is due to the uncertain stoichiometric coefficient of ${\mathrm{Si}}$ in polycide and the possible wide range of the applied doping of the ${\mathrm{polySi}}$ layer, which results in large standard deviations compared to the value for the pure materials.

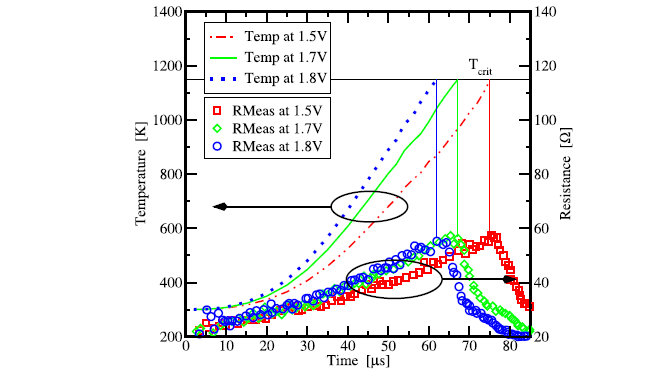
Another interesting outcome of this investigation is that the temperature at which the resistance falls, is the same for all three different applied voltage ramps. Therefore, one can assume that this particular temperature corresponds to a material-specific phenomenon which is related to thermal run-away. This effect is most likely related to an electromigration process in the polycide layer [89,88].

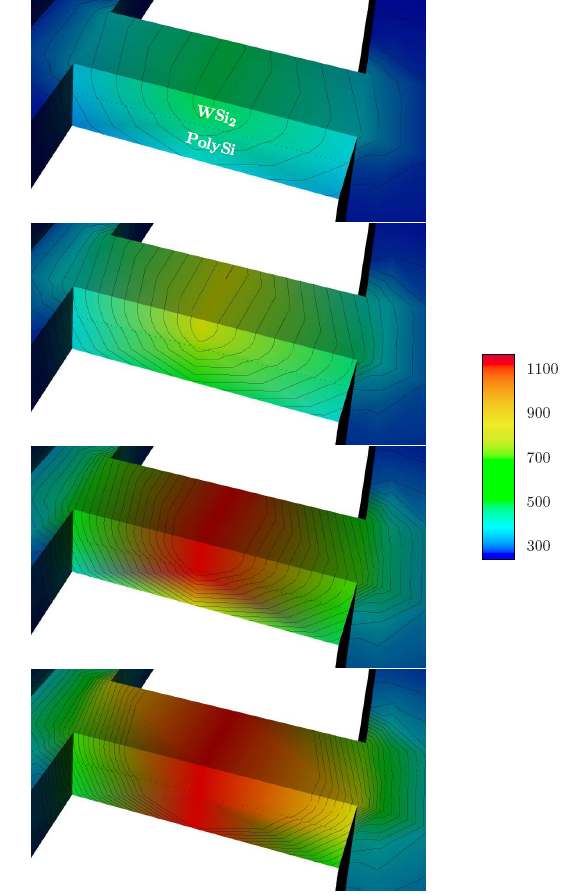
As expected the area with the highest local temperature is located at the surface of the bridge in between the two interconnect pads as shown in Figure 5.16. The extracted parameters can be used for further investigation of local temperature distributions and self-heating effects in other interconnect structures where similar materials are used.

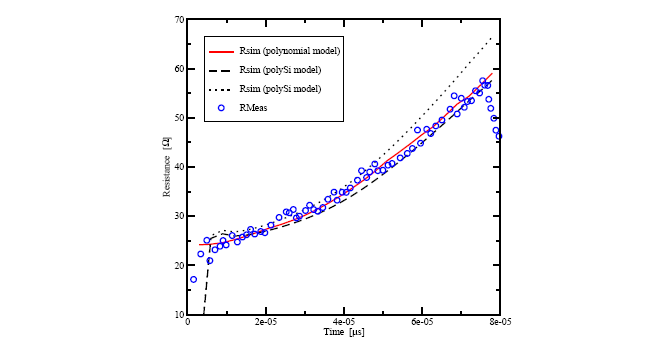
Applying the derived model for ${\mathrm{polySi}}$ from Section 2.5.1, the trend of the characteristic resistance evolution can be very well reproduced. Figure 5.17 shows a comparison between the measured resistance, the calibrated polygonal conductivity model, and the polySi model from Section 2.4.1 which consists of various different materials parameters where the material parameters proposed in [179,180] have been used with the adapted doping concentrations.

However, Figure 5.17 shows the two different parameter sets where only one parameter has been changed by $\pm 2 \%$ . Varying other model parameters offers the possibility to recalibrate the model where their values have no without physical meaning. Thus, without knowledge of the internal materials properties, for instance the distribution of the energy barriers, grain size, trap density at the grain boundary sites, and the thickness of the grain boundary region, the model can be calibrated roughly only. With knowledge of these fundamental material parameters a calibration of this model would yield an excellent match to the experimental data.

Figure 5.14: Comparison of the simulation results with the resistance measurements showing the evolution of the resistance of the fuse.

Figure 5.15: Comparison of the simulation results with the resistance measurements confronting the resistance evolution with the maximum temperature in the fusing structure.

Figure 5.16: The temperature distribution [K] at the hottest spot in the fusing area. It shows that the upper region ($WSi_2$ ) reaches the highest temperature during programming at 32$\mu$ s, 40$\mu$ s, 50$\mu$ s, and 60$\mu$ s.

Figure 5.17: Comparison between the polygonal conductivity model and the polySi conductivity model applied to the fusing structure. For the polySi model two completely different parameters sets have been applied which both show rather a good agreement with the measurements.