2.1 Temperature

To fully describe a complex system on a microstate level, an enormous number of different microstates has to be known, and their interactions have to be determined in order to obtain the future behavior from the past states. Because is not possible to store the bulk of data that would be necessary to calculate all the effects correctly, a statistics-based description has to be used [70]. A possible way to obtain a representative quantity is to count the number of occupied or unoccupied microstates. Historically, the maximum number of possible states which can be theoretical occupied was chosen to determine the disorder of a system. This maximum value of disorder correlates with the energy of the system. Because the number of microstates is always a positive integer and is normally enormously large, the corresponding information content of a given system $\mathcal{S}$ can be logarithmically counted according to information theory. This introduced logarithmic quantity is the so-called entropy ${\sigma}(\mathcal{S})$ which represents the level of maximum disorder.

Hence, the historical definition of the entropy of a given system is a measure for the number of all possible quantum states which can be achieved following a uniform probability distribution. If the number of reachable microstates for a system $\mathcal{S}$ is determined by ${N_{\mathrm{\sigma}}}\in \mathbb{N}$ , the corresponding entropy ${\sigma}$ of this system is defined as its natural logarithm

$\displaystyle {\sigma}(\mathcal{S}) {=}\ln({{N_{\mathrm{\sigma}}}}).$

(2.19)

This entropy ${\sigma}(\mathcal{S})$ is a function of the energy

, the number of particles

, and the volume

of the system because ${N_{\mathrm{\sigma}}}$ depends on these parameters itself.

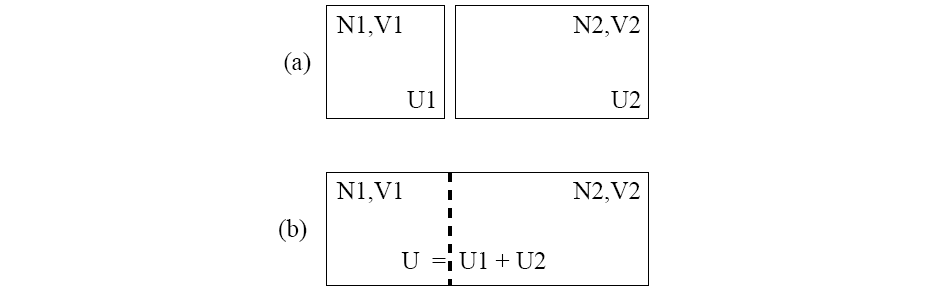
If two systems are considered as spatially and thermally insulated systems $\mathcal{S}_1$ and $\mathcal{S}_2$ , where each of them has a certain internal energy ${{U}}_1$ and ${{U}}_2$ as shown in Figure 2.1a. and if they are brought into thermal contact (cf. Figure 2.1b), the number of particles and the volumes remain constant, but the individual energies ${{U}}_1$ and ${{U}}_2$ are no longer spatially confined [69]. Therefore, an energy transmission can be observed. In this case, the total energy ${U}{=}{{U}}_1 + {{U}}_2$ remains constant if no other energy fluxes are observed. So the energy flows in the most probable case from one side to the other under the constraint that the product of the single entropies ${{N_{\mathrm{\sigma}}}}_1{{N_{\mathrm{\sigma}}}}_2$ maximizes. That is again a measure for the total number of states of the global system and therefore, also the sum

$\displaystyle {\sigma}(\mathcal{S}) {=}\ln({N_{\mathrm{\sigma}}}{}_1 {N_{\mathrm{\sigma}}}{}_2) {=}{{\sigma}}_1 + {{\sigma}}_2$

(2.20)

increases.

**Figure 2.1:** Two separately isolated subsystems (a) are brought into thermal contact (b). The number of particles and the volume remains constant for each system but the energy can be exchanged through the thermal contact.

After a certain time, the energy fluctuation from one side to the other becomes zero in average. Hence, these two systems $\mathcal{S}_1$ and $\mathcal{S}_2$ are in a state of thermal equilibrium if the equation

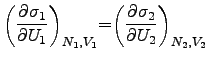$\displaystyle \displaystyle{\left(\frac{\partial{{\sigma}}_1}{\partial{{U}}_1}\... ...} {\left(\frac{\partial{{\sigma}}_2}{\partial{{U}}_2}\right)}_{{{N}}_2,{{V}}_2}$

(2.21)

holds for the whole system $\mathcal{S}({U})$ . Here, ${{U}}_i$ and ${{\sigma}}_i$ are the energy and the entropy of the system

. This property of equivalence in the thermal equilibrium is exactly what we expect to be the temperature. Therefore, the fundamental temperature ${\tau}$ is thermodynamically defined as

$\displaystyle \frac{1}{{\tau}} {=}\frac{\partial{{\sigma}}}{\partial{{U}}} \quad \Longrightarrow \quad {\tau}{=}\frac{\partial{{U}}}{\partial{{\sigma}}},$

(2.22)

where the fundamental temperature $\tau$ has the unity of an energy. Determining ${\tau}$ to be the reciprocal of ${\partial{{\sigma}}}/{\partial{{U}}}$ guarantees that energy flows from the system with higher ${\tau}$ to the system with lower ${\tau}$ . The temperature

is measured in Kelvin and is proportional to ${\tau}$ by the equation

$\displaystyle {\tau}{=}{k_{\mathrm{B}}}{T},$

(2.23)

where ${k_{\mathrm{B}}}$ is BOLTZMANN's constant and therefore, the conventional entropy

is defined as

$\displaystyle {S}{=}{k_{\mathrm{B}}}{\sigma}.$

(2.24)

Hence the conventional temperature can be expressed as

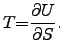$\displaystyle T {=}\frac{\partial{{U}}}{\partial{{S}}}.$

(2.25)

An interesting corollary to definition (2.22) is the fact that the value zero for the fundamental temperature cannot be reached under the constraint of finite energy resources because the energy gradient would become infinity which has been proven to be impossible [71].

Stefan Holzer 2007-11-19