The LEVENBERG-MARQUARDT algorithm [242] is an efficient
method to solve non-linear least squares problems [243]. Thus, it
is well suited for complex inverse modeling tasks especially for TCAD
applications where the aim of the LEVENBERG-MARQUARDT algorithm is to
optimize (minimize) a twice differentiable function
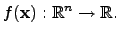 |
(4.22) |
If the original objective function is vector valued, an additional norm has to
applied to map the vector to a scalar-valued quantity.
The second derivative of the function 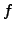 is determined by its HESSian4.6 matrix. Because the optimization tasks for TCAD
problems cannot be described analytically, the derivatives have to be
calculated for each single point.
Since there is no guarantee that the HESSian
is determined by its HESSian4.6 matrix. Because the optimization tasks for TCAD
problems cannot be described analytically, the derivatives have to be
calculated for each single point.
Since there is no guarantee that the HESSian
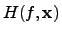 is positive
definite for non-quadratic forms, the search algorithm might search in the wrong
direction. Therefore, a correction term can be introduced to cover this
problem by [242]
is positive
definite for non-quadratic forms, the search algorithm might search in the wrong
direction. Therefore, a correction term can be introduced to cover this
problem by [242]
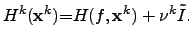 |
(4.23) |
If
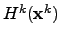 is still not positive definite, the factor
is still not positive definite, the factor 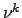 is increased
by a certain user-defined factor.
Since
is increased
by a certain user-defined factor.
Since
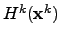 is now per definitionem positive definite, the next point
is now per definitionem positive definite, the next point
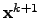 can be calculated by
can be calculated by
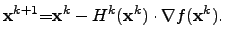 |
(4.24) |
However, if there is no improvement in the last minimization step (
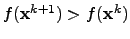 ), the factor
), the factor 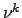 has to be modified again and the previously
described steps have to be recalculated.
has to be modified again and the previously
described steps have to be recalculated.
This method is a more robust method than the GAUSS-NEWTON
method [244] and provides in general an optimum on less
iterations. Nevertheless, if the initial guess of
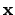 is too close to the
optimal value, the convergence might be slower than that of the
GAUSS-NEWTON method.
is too close to the
optimal value, the convergence might be slower than that of the
GAUSS-NEWTON method.
Stefan Holzer
2007-11-19
![]() is too close to the
optimal value, the convergence might be slower than that of the
GAUSS-NEWTON method.
is too close to the
optimal value, the convergence might be slower than that of the
GAUSS-NEWTON method.