Black Box Approach

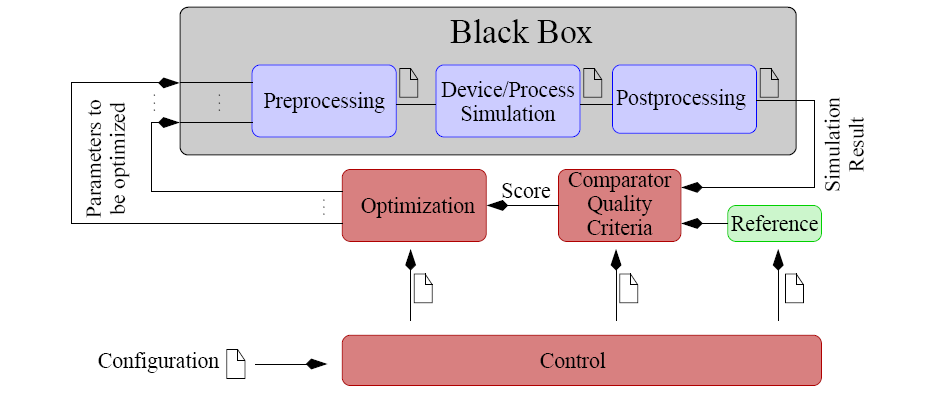
Figure 4.4: Data flow for the optimization mode in SIESTA. The base structure is shown with the external simulation sequence depicted as interchangeable black box.

In TCAD applications, most of the problems cannot be formulated using one single set of equations. Due to the steadily increasing complexity of the material models and the physical effects which have to be considered, the behavior might change if a certain quantity has exceeded a certain value. For instance if the temperature has reached the melting point of ${\mathrm{Al}}$ , the conductivity model looses its validity or if the electric field exceeds a certain threshold, a breakdown of the dielectric occurs. Both scenaria requires a switch of the models in the simulator. Therefore, optimization methods which use information about the shape and gradients are very difficult to apply due to the uncertainty of hidden constraints and due to suboptimal discretizations. As an alternative, the objective function, which includes the simulation as well as the score function, can be assumed to be a black box function where only the values of the function at a certain point are known. For this case the standard optimization methods have to calculate the gradient separately which is very time-consuming if the parameter space is of a high dimension. Thus, a gradient-free optimization strategy would be appropriate for this case.