4.3.1 Design of Experiments

Figure 4.5: Two propaedeutic example designs with three input parameters. The central composite circumscribed (CCC) design is shown in (a) and the central composite face-centered (CFC) design in (b).

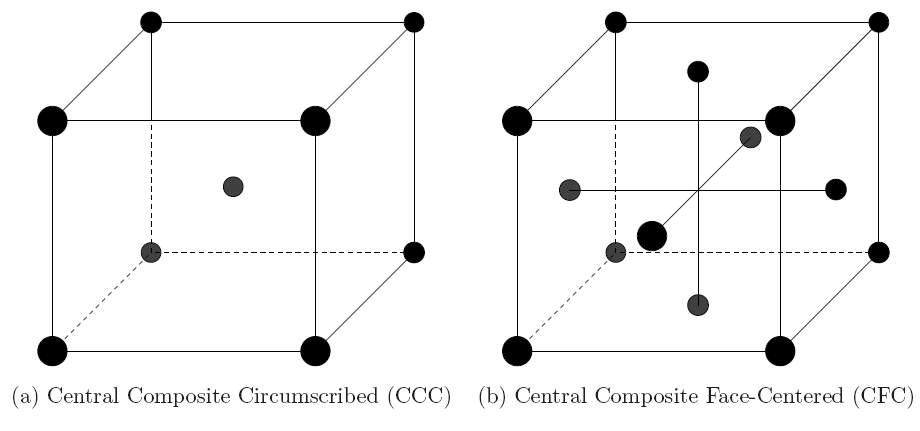
As a result of a rigorously investigated problem nearly all parameter combinations have to be evaluated for the worst case to determine and verify the global optimum of a particular problem. Since this procedure to obtain the necessary information is very time consuming a very effective design of experiment (DOE) method has been introduced in the industry.

In this method a DOE tool proposes sets of parameters which cover the complete discretized parameters space of a certain problem. These collected results of the parameter sets can be filed, for instance in a data base, and further data manipulation routines can be applied on this data. A common use is to provide this type of data for design environments to check if the desired arrangements of parameters from the user results in reasonable and manufacturable devices.

However, the computation effort cannot be reduced because the parameter evaluations have to be performed to obtain the optimum. Adding additional parameter evaluations and storing them to a database enables the use of the information obtained from the optimization. So, the engineers can use the information obtained from previously run experiments and save a lot of time and computational resources.

There are several methods to distribute parameter sets (designs, experiments) into the parameter space [284,44]. One possible way is to select the parameters randomly around a certain expected mean value. The full factorial design divides each parameter axis in $m$ sections which results in $m^n$ different designs to evaluate, where $n$ is the dimension of the input parameter domain (hypercube). The sectioning of the hypercube can be chosen according to the featured transformation of the tools used in the DOE. Common transformation are given in Tab. 4.1 where the principle behavior of the parameters can be accounted for. For instance, typical doping concentrations may vary by several orders of magnitudes. Hence, a logarithmic transformation is usually more suitable than a equidistant linear distribution of the designs.

Table 4.1: Common transformations for designs (cf. for instance [44,40]).

Parameter	Description
default	equidistant
linear	$$a x+b$$
logsimple	$$\log{(x)}$$
logarithmic	$$a \log{(b x)}$$
function1	$$A \log{\left(\frac{x}{B}\right)}$$
function2	$$A \frac{x - B}{x}$$
function3	$$B \exp{\left[A \frac{x-C}{C}-1\right]}$$
function4	$$B \left(1 - \exp{\left[A \frac{C-x}{C}\right]}\right)$$